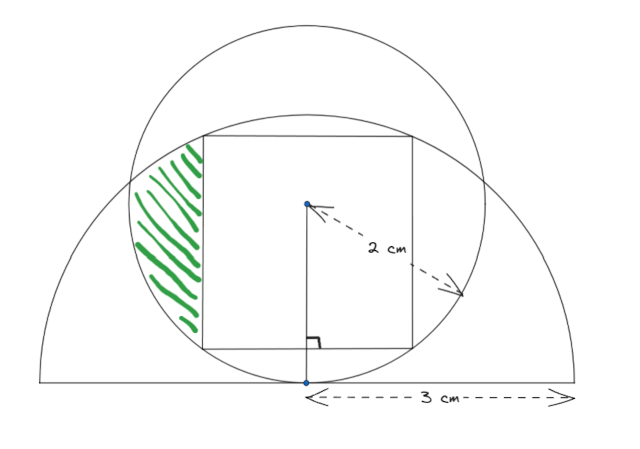
The answer to the question is \(1.349\).
In the first step, we find the length of the sides of the square, which is approximately 2.36822, and the x coordinate of the left side of the square which is \(x_4 \simeq -1.18411\). In the second step, we find the area of the intersection of the red circle and the green semicircle. We know that \(y_3 = 2.25\). Now, putting it in the semicircle formula, we get: \[x_3^2+y_3^2 = 3^2 \quad \implies \quad x_3 \simeq -1.98431\] Now, if we look closely at the target area, it can be divided into 3 parts:

• green section which is located between the green semicircle and the line \(x=2\).

• red section which is located between the line \(x=2\) and the lower half of the red circle.

• blue section which is located between the upper half of the red circle and the line \(x=2\).

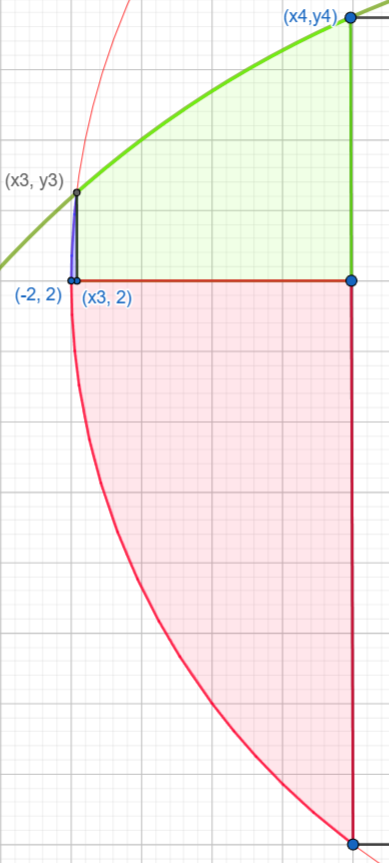
Now we get the area of each part by integral: \[\begin{aligned} A(\textsf{blue}) &= \int_{-2}^{x_3}\sqrt{4-x^2}dx \simeq 0.00262 \\ A(\textsf{green}) &= \int_{x_3}^{x_4}\sqrt{9-x^2}-2 dx \simeq 0.42644 \\ A(\textsf{red}) &= \int_{-2}^{x_4}2 - (-\sqrt{4-x^2} + 2) dx \simeq 0.92011 \end{aligned}\] By adding the above three values, the answer to the problem is approximately 1.349.