Oppenheimer ticket queue

40 people are standing in a line in front of a cinema to buy tickets
to the Oppenheimer movie. The ticket price is 5 dollars. Out of these 40
people, 25 of them have only 5 dollar bills and 15 of them have only 10
dollar bills. The cashier has no cash in the beginning, however, when
people start purchasing tickets she will collect cash based on what they
give her. Indeed, the price of the ticket is 5 dollars and if a person
gives a 10 dollar bill to the cashier, she has to return a 5 dollar
bill. How many different permutations of people will allow the cashier
to always give a 5 dollar bill to the people who only have 10 dollar
bills?
Link to the problem on Twitter: https://twitter.com/Riazi_Cafe/status/1691691003118596147
The correct answer is \((\binom{40 }{25} -
\binom{40}{26}) \cdot 25! \cdot 15!\).
Let \(m\) be the number of people who
have \(5\) dollar bills and \(n\) be the number of people who have \(10\) dollar bills. We show the
configuration of a permutation of the people in the queue with a diagram
similar to the one below, where we start from the origin and if the next
person has \(5\) dollar bills, we go to
the top right, and if he only has \(10\) dollar bills, we go to the bottom
right.
In order to keep the diagram small, instead of \(m=25\) and \(n=15\) for the main problem, we show an example diagram for \(m=6\) and \(n=4\).
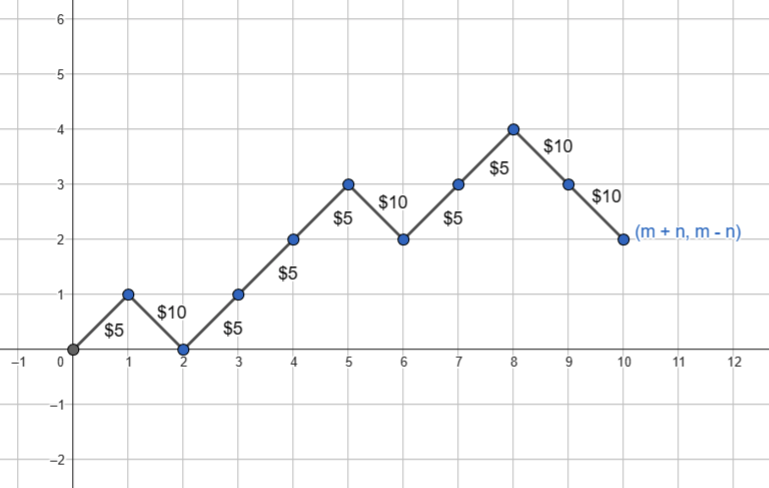
The number of such graphs is \({n+m \choose m}\). Notice that a configuration is acceptable, only if we never go below line \(y=0\). An example of an unacceptable configuration is given below.
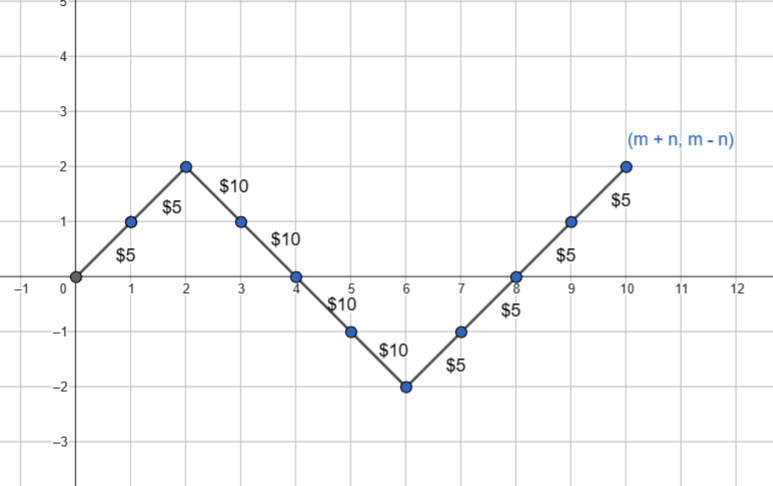
To count these unacceptable configurations, we observe that these states are the states where the graph intersects the line y=-1. We show a 1-to-1 mapping between such figures and the ones that start from location \((0,-2)\). To this end, we mirror the graph before the first intersection with line \(y=-1\). For example, for the figure above the result would be as follows:
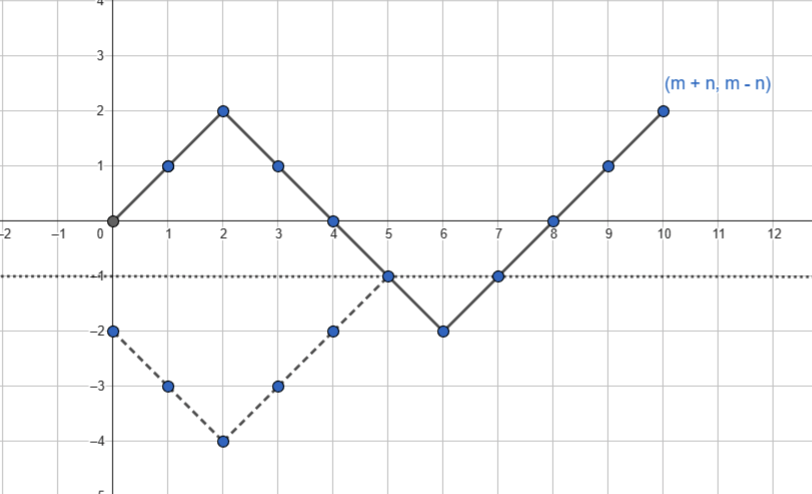
Notice that in all such graphs we start from point \((0,-2)\) and end at \((m+n, m-n)\) as before. These diagrams have a one-to-one correspondence with unacceptable states. Thus, the number of such configurations is to \({n+m \choose m+1}\).
So the total number of acceptable configurations is equal to \({n+m \choose m} - {n+m \choose m+1}\). In these configurations, we are indifferent between people who have the same set of bills. If we also take into account such distinctions, the answer would be the following:
\[\left({n+m \choose m} - {n+m \choose m+1}\right) \times n! \times m!\]