Heshmat and Gholi
This is a modified version of one of the IMO 2023 problems.
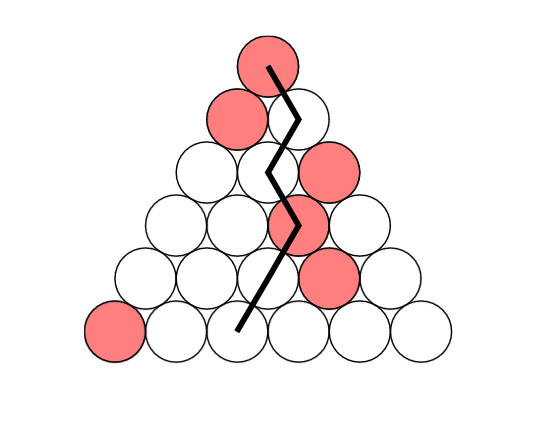
We have 1369 lines of balls; In each line \(i\), there are \(i\) balls placed next to each other. The
\(j\)’th ball of each line is connected
to the \(j\)’th and \(j+1\)’th balls of the next row. A ninja
path consists of 1369 balls from different lines, where balls of
consecutive lines are connected (see an example in the figure).
Heshmat selects one ball from each line and colors them with red.
Afterwards, Gholi finds a ninja path that contains the most number of
red balls. If Heshmat does not cooperate with Gholi, what is the minimum
number of red balls of Gholi’s ninja path?
Link to the problem on Twitter: https://twitter.com/Riazi_Cafe/status/1699307153184739688
The answer to question is 11.
To show this, we need to prove two propositions: The first proposition
is that there is a method for Heshmat that if he colors the balls in
such a way, the number of red balls in every ninja path will be at most
11. The second proposition is that no matter how Hashmat colors the
balls, there is a ninja path with at least 11 red balls. Let us first
show the first proposition. Consider the following coloring method:
| line \(1 \rightarrow 1\) |
| line \(2 \rightarrow 1\) |
| line \(3 \rightarrow 3\) |
| line \(4 \rightarrow 1\) |
| line \(5 \rightarrow 3\) |
| line \(6 \rightarrow 5\) |
| line \(7 \rightarrow 7\) |
| line \(8 \rightarrow 1\) |
| \(\vdots\) |
In the above coloring method we iterate over lines and color one ball from each line. We start by coloring the first ball of the first line. From then on, for each next line, we move two balls to the right and color the ball if it exists. Otherwise we continue on by coloring the first ball of the current line and repeat the same process for the next lines. In other words, for each line \(2^i\) we color ball number 1, and for lines \(2^i +j\) we color ball number \(1+2j\) (\(j < 2^i\)).
Due to our coloring, from each interval of lines \([1,1], [2,3], [4,7], \ldots, [512,1023], [1024,1369]\) there will be a maximum of one colored ball per ninja path. Thus, no ninja path can have more than 11 red balls.
Next, we show the second proposition. In other words, we show that for every coloring of Heshmat, there is a ninja path for Gholi with at least 11 colored balls.
For this we leverage the Dilworth theorem below: Theorem 1. [Dilworth theorem, https://en.wikipedia.org/wiki/Dilworth%27s_theorem] In any finite partially ordered set, the largest antichain has the same size as the smallest chain decomposition.
The Dilworth theorem shows that if there is no ninja path with 11 red balls for some coloring, then the line can be divided into 10 groups such that no two red balls in lines of a group are reachable from one another. In other words, if lines \(i\) and \(j\) are in the same group and their red balls are at positions \(a\) and \(b\), then we have \(|a-b| > |i-j|\). One can see that this is impossible since \(2^{10} < 1369\).