Right Triangles

Two right triangles \(ABZ\) and \(DBZ\) are given with the edges lengths below:
\(\bar{ZA}=33\)
\(\bar{BD} =16\)
\(\bar{BZ}=65\)
What is the the length of \(\bar{TH}\).
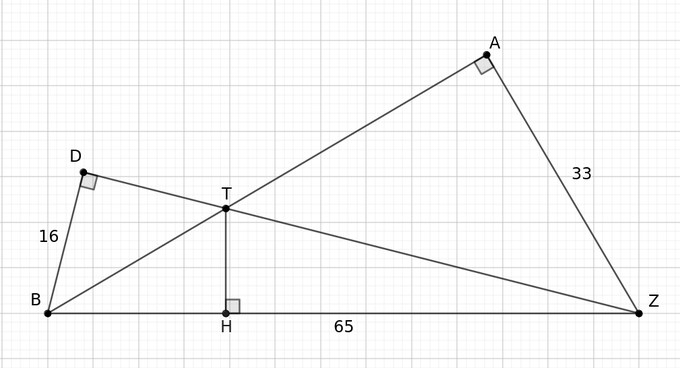
Link to the problem on Twitter: https://twitter.com/Riazi_Cafe/status/1701844480939397217
The answer is equal to \(y \approx
11.53613\).
According to the Pythagorean theorem, we have \(\bar{AB}=56\) and \(\bar{DZ}=63\). Considering \(B\) as the origin, we formulate the lines
\(\bar{AB}\) and \(\bar{DZ}\) as below. The \(y\) coordinate of the intersection of these
two lines is equal to the answer.
\[\begin{align} \left. \begin{aligned} BA:& y = \frac{33}{56} x \\ DZ:& y = -\frac{16}{63}(x - 65) \end{aligned} \right\} \quad &\implies \quad x \approx 19.57647, y \approx 11.53613 \end{align}\]