Pipe Drilling
The red curve here is defined by \(y = 2x^2\) and the circle is surrounded by the curve and the line \(y=1\). What are the coordinates of the center of the circle and the radius of the circle?
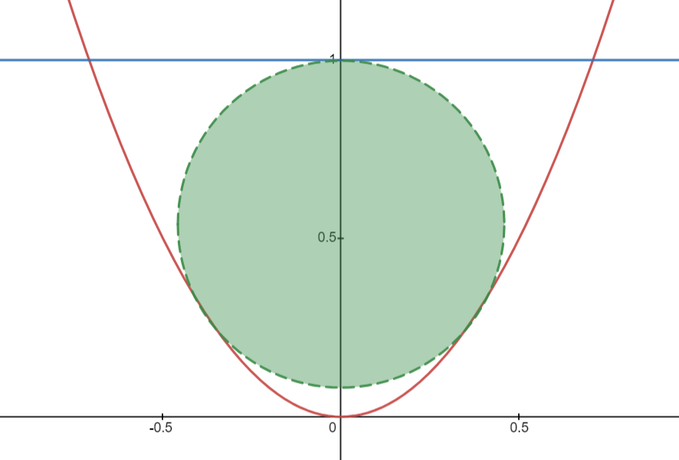
Link to the problem on Twitter: https://twitter.com/Riazi_Cafe/status/1705827665717137521
The center of the circle is approximately equal to \((0,0.542)\) and radius of the circle is
approximately equal to 0.4571.
According to the definition, the curve \(y=2x^2\) is the geometric location of the
points that are of the same distance from the focus with coordinates
\(F: (x=0, y=1/8)\) and the directrix
with the relation \(y=-1/8\).
Therefore, in the diagram below, \(\bar{FP}=\bar{AP}\) and their adjacent
angles in the formed triangle are equal.
Also, by the symmetry of parabola, the segments \(BP\) and \(FP\) make an equal angle with the segment perpendicular to the parabola at the point \(P\), and according to the property of the circle, the segment perpendicular to the point \(P\) is the radius of the circle.
Thus the angles marked in the figure are equal, and \(CFAP\) is a parallelogram, and therefore \(\bar{CF}=\bar{AP}\), from which we can conclude \(C_y=P_y+1/4\).
\[\begin{aligned} CF = AP \implies& \\ C_y - F_y = P_y - A_y \implies& \\ C_y - \frac{1}{8} = P_y + \frac{1}{8} \implies& C_y=P_y+\frac{1}{4} \end{aligned}\]
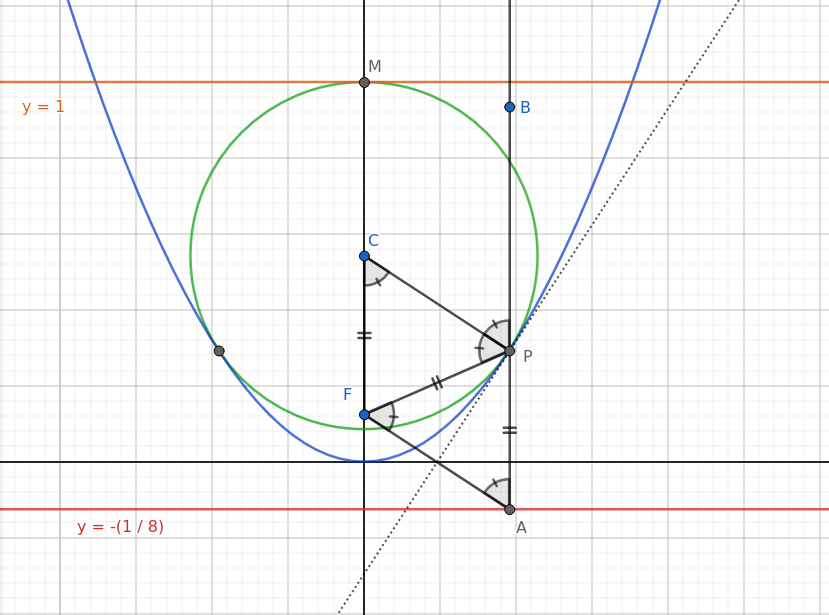
On the other hand, the radius of the circle is equal to \(1-C_y\). Therefore \(\bar{CP}=1-C_y\). If we put this next to \(C_y=P_y+1/4\), we can determine \(C_y\) and \(R\).
\[\begin{aligned} CM = CP \implies& (1 - C_y)^2 = (C_y - P_y)^2 + (0 - P_x)^2 \\ \implies& (1 - C_y)^2 = \frac{1}{4}^2 + \frac{P_y}{2} \\ \implies& 1 - 2C_y + C_y^2 = \frac{1}{4}^2 + \frac{C_y-1/4}{2} \\ \implies& C_y^2 - \frac{5}{2}C_y + \frac{17}{16} = 0 \\ \implies& C_y = \frac{5}{4} - \frac{1}{\sqrt{2}}, R = \frac{1}{\sqrt{2}} - \frac{1}{4} \end{aligned}\]