. The answer to both cases of the problem is equal to \(5\).
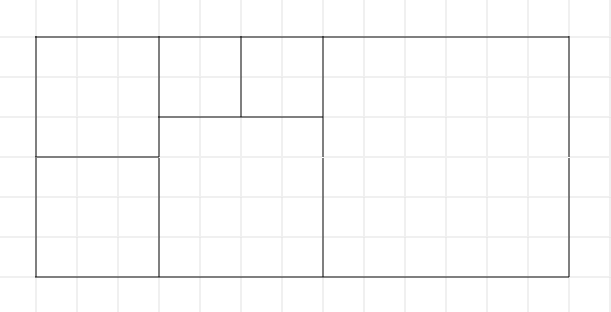
\(6 \times 13\) case:

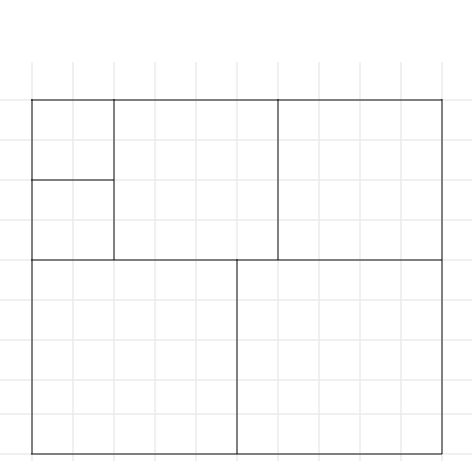
\(9 \times 10\) case:

Below we explain why 5 cuts are necessary in both cases. Keep in mind that the only case where no cut is necessary is when the starting rectangle is already a square. We can solve the problem with one cut only if the starting rectangle has dimensions \((x,2x)\) or \((2x,x)\) for some integer \(x\). Also, the only cases where the problem is solvable with two cuts are the ones whose original rectangle has dimensions \((x,1.5x)\) or \((1.5x, x)\) for some even \(x\) or dimensions \((x,3x)\) or \((3x,x)\) for some integer \(x\). Keep in mind that none of the cases of our problem fall in any of these categories and thus 3 cuts are necessary to cut the original rectangles in each case.

The only way we can solve the problem with 4 cuts is if after the first two cuts, we end up with either (i) two squares and a rectangle that can be divided into squares with 3 cuts or (ii) one square and two rectangles whose dimensions are \((x,2x)\) or \((2x,x)\) and \((y,2y)\) or \((2y,y)\) for some integer \(x\) and some integer \(y\). Moreover, the total area of these rectangles should be equal to the area of the original rectangle. For the \(6 \times 13\) case, there are only two combinations of such rectangles whose total area is \(6\cdot 13 = 78\) (we ignore the cases that are identical up to rotation by 90 degrees):

• (2, 2), (1, 2), (6, 12),

• (6, 6), (6, 6), (2, 3).

Obviously, there is no way to decompose a \(6 \times 13\) rectangle into either combination with 2 cuts. Thus we need at least 5 cuts to solve the first problem.

Similarly, there are three such combinations for the \(9 \times 10\) case whose total area are equal to \(9\cdot 10=90\).

• (1,1), (2,2), (3,9)

• (4, 4), (1, 2), (6, 12)

• (8, 8), (2, 4), (3, 6)

Again, none of the combinations is constructable with two cuts starting from a \(9 \times 10\) rectangle.