Cubic Hole

We are given a wooden cube with sides of length 1cm. We can drill the
cube and create some holes of arbitrary shapes inside it. We then want
to pass the largest possible cube thought the holes of the original
cube. How would you drill the holes and what is the largest possible
cube that can go through the holes?
More details: The figure below shows an example of
drilling the cube (The intersection of the cylinder and the cube is
removed from the cube).

The cube should be drilled in a way that a thread can be passed through it and the cube can be hung by tying the two ends of the thread so that it cannot be pulled down without cutting the thread.
For example, in the figure below, you cannot hang the cube by tying the two ends of the thread.

The passage of the second cube through the first cube should be such that the second cube can make a full circle around the hypothetical thread from which the first cube is hanging.
This problem is called the Prince Rupert’s cube problem. The length
of the largest cube that can go through the original cube is \(\frac{3\sqrt{2}}{4} \approx
1.0606601\).
Place two points on two adjacent edges of a unit cube, each at a
distance of 3/4 from the point where the two edges meet, and two more
points symmetrically on the opposite face of the cube. Then these four
points form a square with side length \(\frac{3\sqrt{2}}{4} \approx
1.0606601.\)
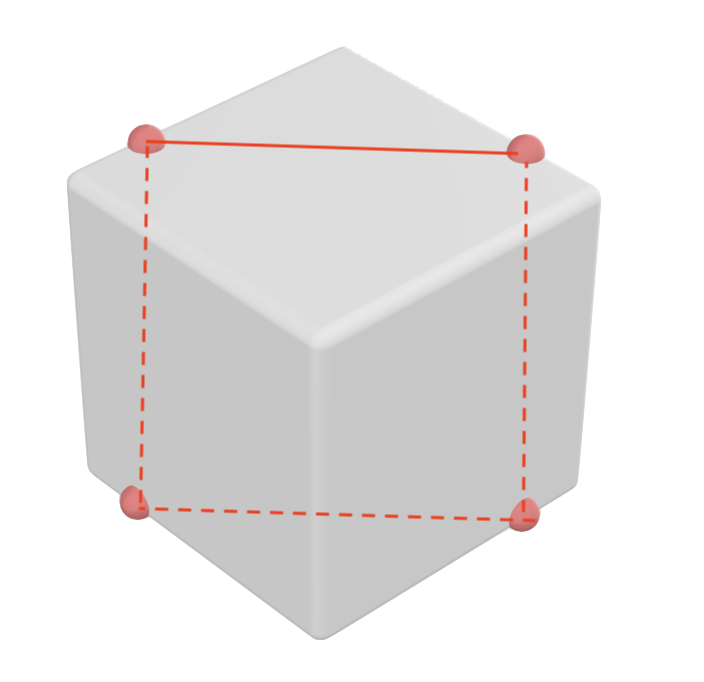
Notice that these four points make a square of length \((3\sqrt{2})/4\). Extruding the square in both directions perpendicularly to itself forms the hole through which a cube larger than the original one, up to side length \((3\sqrt{2})/4\), may pass.