Division
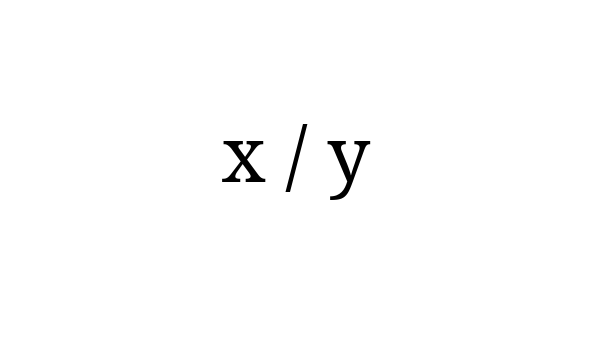
We select two random numbers \(x\) and \(y\), between 0 and 1 uniformly. What is the probability that the nearest integer number to \(x/y\) is even?
Let us define a variable \(r = x/y\) for randomly selected variables \(x\) and \(y\). We also define probability function \(f(a,b)\) as \[f(a,b) = \mathsf{Pr}(a \leq r \leq b).\] With this definition, the answer to the problem would be equal to \(f(0,0.5) + f(1.5, 2,5) + f(3.5,4.5) + \ldots\). Therefore the answer boils down to determining the value of \(f(a,b)\) for arbitrary \(a\) and \(b\). To this end, we consider two cases separately (i) both \(a\) and \(b\) are smaller than 1. (ii) both \(a\) and \(b\) are larger than 1.
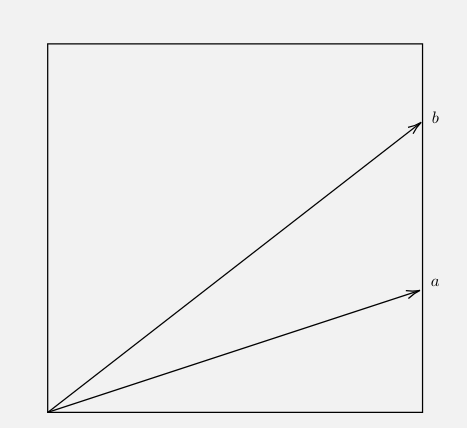
case (i): both \(a\) and \(b\) are smaller than 1: Now, consider a point \(p = (x,y)\) whose coordinates are equal to \(x\) and \(y\). This point is on a unit square that covers points with coordinates between 0 and 1. However, \(x/y\) would be in range \([a,b]\) if and only if the point is on triangle made by the two arrows. Since the area of the triangle is equal to \(\frac{b-a}{2}\) and the area of the square is 1 then the probability that \(a \leq x/y \leq b\) holds is \(\frac{b-a}{2}\).
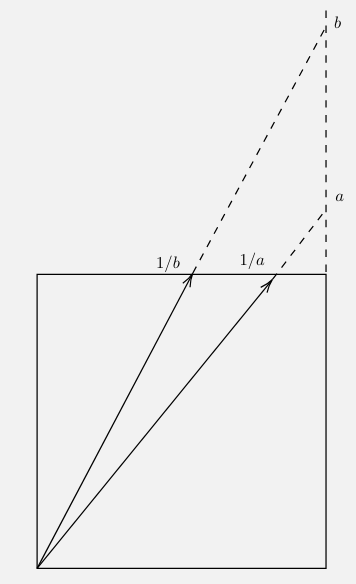
case (ii): both \(a\) and \(b\) are larger than 1. This case is also similar to the previous case except that ratio \(x/y\) would be between \(a\) and \(b\) only if point \(p\) is on the triangle shown in the figure below. Notice that the area of this triangle is equal to \(\frac{1/a - 1/b}{2}\). Thus, the probability that \(x/y\) is between \(a\) and \(b\) is also equal to \(\frac{1/a - 1/b}{2}\).
Based on the arguments above, the answer of the problem is equal to \[\begin{aligned} f(0,0.5) + \sum_{i=1}^{\infty} f(2i-0.5, 2i+0.5) &= 0.25 + \sum_{i=1}^{\infty} \frac{1/(2i-0.5) - 1/(2i+0.5)}{2} \nonumber \\ & = 0.25 + \sum_{i=1}^{\infty} (1/(4i-1) - 1/(4i+1)) \nonumber \\ & = 0.25 + \sum_{i=2}^{\infty} (-1)^i/(2i-1) \nonumber \\ & = 0.25 + 1-\pi/4 \quad \quad \quad \quad \quad \quad\quad \quad \quad \text{(1)}\\ & = 1.25-\pi/4 \nonumber \end{aligned}\] where (1) is based on the Leibniz formula (\(\pi/4 = 1-1/3 + 1/5 - 1/7 \ldots\)).