امروز به جای مساله، یه متن کوچولوی آموزشی داریم.

اگه n تا شهر داشته باشیم، می‌تونیم با کشیدن n-1 جاده بین‌شهری، شبکه‌ای بسازیم که هر شهری به هر شهر دیگه مسیر داشته باشه. این جاده‌کشی رو می‌تونیم n^(n-2) جور انجام بدیم.

مثلا ۱۶ حالت جاده‌کشی برای ۴ شهر رو می‌بینین.

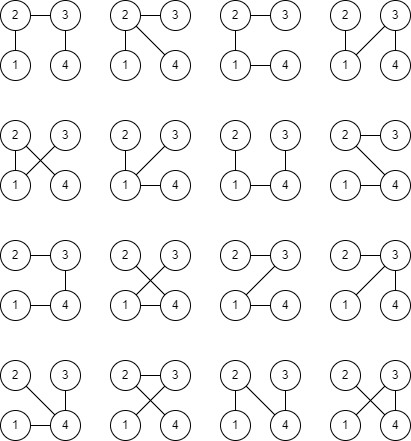
امروز به یه اثبات ساده برای فرمول تعداد حالات نگاه می‌کنیم.

یه کدگذاری هست به نام پروفر که میشه نشون داد هر عضوش تناظر یک به یک داره با شبکه با شرایط بالا. ولی شمردنش آسونتره. به خاطر این تناظر یک به یک، اگه تعداد کدهای پروفر رو بشمریم، در واقع تعداد شبکه‌ها رو شمردیم.

برای محاسبه این کد، از بین شهرایی که سر فقط یه جاده هستن اونی که عددش کمتره رو پیدا می‌کنیم (مثلا A)، شماره اون سر دیگه جاده رو یادداشت می‌کنیم، و سپس خود A رو حذف می‌کنیم. این کار رو هی تکرار می‌کنیم تا فقط ۲ شهر بمونه. این شماره شهرایی که یادداشت کردیم میشه کد پروفر.

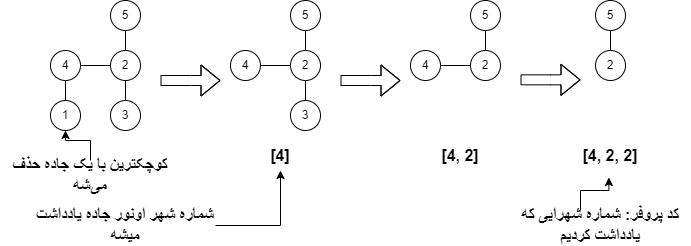
جالبیش اینجاست که اگه این کد رو داشته باشیم، خود شبکه رو می‌تونیم بازسازی کنیم! که این بخش رو و کامل کردن اثبات تناظر یک به یک رو به عنوان تمرین میذاریم برای شما. حال چون این دنباله طولش n - 2 و برای هر عضوش n تا انتخاب داریم و تکرار هم مجازه، تعداد این دنباله‌ها میشه n ^ (n-2).