مسئله بازل از سوال‌های جالبی بود که برای اولین بار توسط پیترو منگولی در قرن ۱۷ مطرح و حدود ۸۵ سال بعد با نبوغ امیر ریاضیات، لئونارد اویلر حل شد. علت نام‌گذاری هم به شهر زادگاه اویلر و برنولی برمی‌گرده که هر دو برای حل مسئله تلاش کردن.

\[\sum_{n=1}^{\infty}\frac{1}{n^2}=\frac{\pi^2}{6}\]

چالش این مسئله اینه که چجوری ممکنه جمع تعدادی عدد گویا به یک عدد گنگ میل کنه، تازه اونم توان دوم پی تقسیم بر ۶!

در ادامه قراره یک اثبات بسیار زیبای هندسی رو برای این مسئله توضیح بدم. ایده‌ی کلی اثبات ساخت سری روی دایره هست. این ایده به خاطر وجود عدد π الهام گرفته شده.

\[1 + \frac{1}{4} + \frac{1}{9} + \frac{1}{16} + \frac{1}{25} + ... = \frac{\pi^2}{6}\]

این اثبات توسط Johan Wästlund در سال ۲۰۱۰ انجام شده که لینکش رو برای مطالعه بیشتر گذاشتم (http://math.chalmers.se/~wastlund/Cosmic.pdf). همونطور که گفتم هر جا عدد π هست باید یه ارتباطی هم با دایره وجود داشته باشه. چون از اساس عدد π محیط دایره‌ای با قطر ۱ تعریف شده و به نوعی مفهومش با دایره عجینه.

برای شروع فرض کنیم شنونده‌ای روی نقطه صفر محور ایستاده. رو به روی اون و به ترتیب روی نقاط ۱،۲،… بلندگویی قرار می‌دیم. چون امواج صدا با فاصله‌ ما از اون‌ها رابطه‌ی عکس دارن، میزان صدایی که از هر بلندگو شنیده می‌شه رو به دلخواه عکس مجذور فاصله شنونده تا هر بلندگو تعریف می‌کنیم.

پس صدایی که از بلندگوی اول شنیده می‌شه ۱ واحد، بلندگوی دوم یک‌چهارم واحد، سومی یک‌نهم واحد، و به ترتیب تا انتها. اینجوری مجموع صدایی که از همه‌ی این بلندگوها شنیده می‌شه برابره با جمع تک‌تک این اعداد که یعنی همون مسئله‌ی معروف بازل. اما این مدل‌سازی سوال چه سودی برای ما داره؟

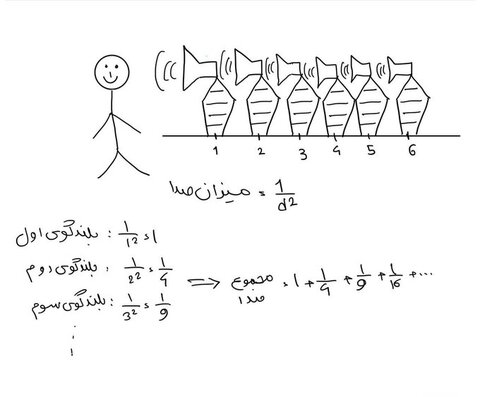
با همین فرایض مسئله رو ادامه می‌دیم. این‌بار فرض کنیم شنونده‌ در نقطه‌ی A ایستاده و بلندگوی اول رو در نقطه‌ی B، اون طرف دایره‌ای با محیط ۲ و قطر ۲ روی π قرار می‌دیم. این دایره ۲ کمان به اندازه‌ی ۱ می‌سازه. همچنین طبق محاسبات، میزان صدایی که از اون به گوش می‌رسه برابره با π²/4.

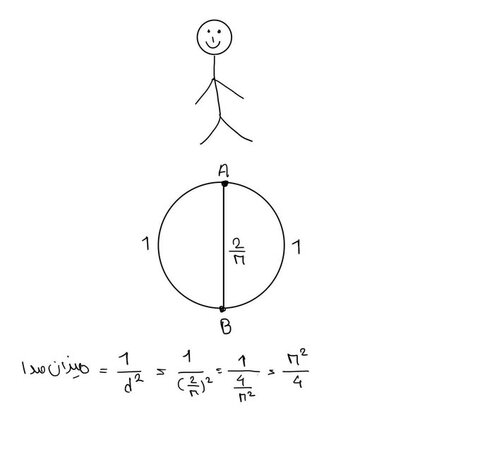
از تکنیک جالبی استفاده می‌کنیم؛ دایره‌ای دو برابر بزرگتر از فعلی، با محیط ۴ رسم می‌کنیم. از نقطه‌ی B که مرکز دایره دومه خط مماسی به دایره اول رسم می‌کنیم تا بزرگه رو در نقاط C٫D قطع کنه. CD قطر دایره دومه، پس مثلث ACD توی A قائمه‌س و می‌شه از قضیه‌ی وارون فیثاغورس استفاده کرد.

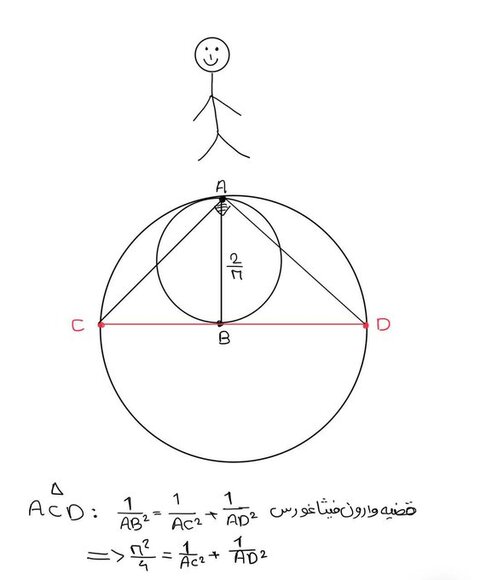
حالا بلندگوی اول رو برداشته و جاش در نقاط C,D دو بلندگوی جدید قرار می‌دیم. رابطه‌ی قبل تضمین می‌کنه مجموع صدایی که از این دوبلندگو شنیده می‌شه همچنان π²/4 هست. در مرحله‌ی بعد دایره‌ای دوبرابر بزرگتر با محیط ۸ رسم می‌کنیم. از C و D هم خطی به B رسم کرده و از دوطرف ادامه می‌دیم.

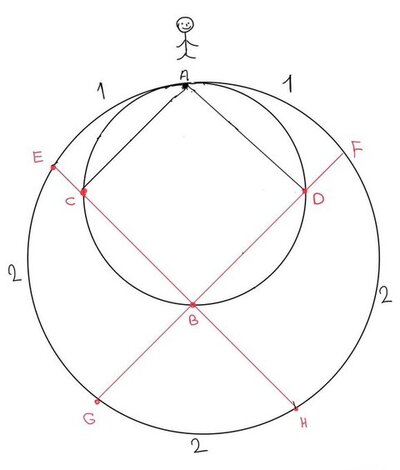
خطوط GF و EH قطر دایره‌ی جدید هستن. نتیجتاً مثلث‌های AEH و AGF توی‌ راس A قائمه می‌شن. دوباره از قضیه‌ی وارون فیثاغورس توی این مثلث‌ها استفاده می‌کنیم. این روابط نشون می‌دن که می‌شه به جای بلندگوی C از E,H و به جای D از F,G استفاده کرد؛ پس مجموع صدای این ۴ بلندگو هم π²/4 هست.

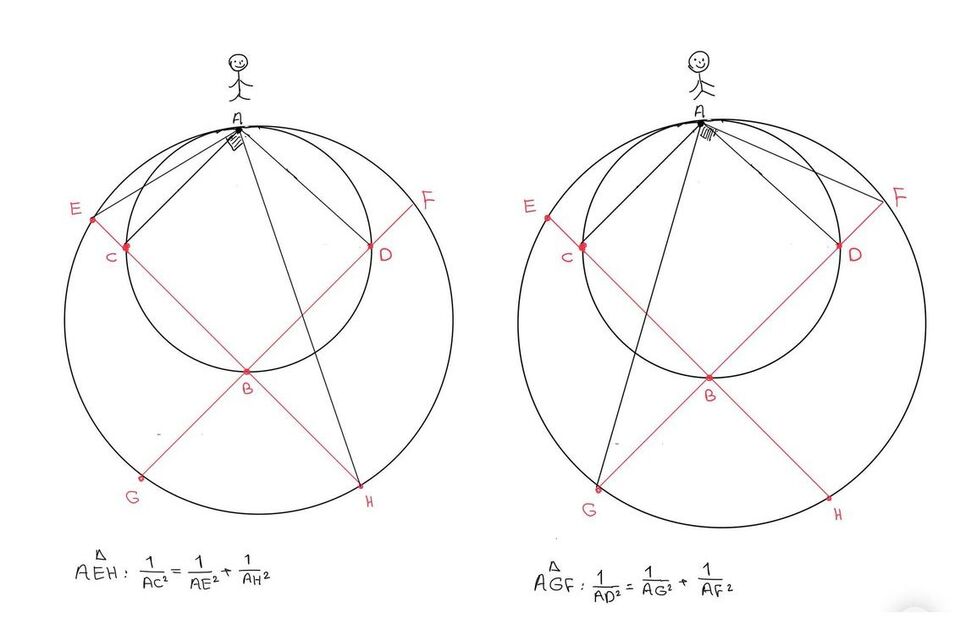
یده‌ی ادامه‌ی کار هم دقیقاً مشابه قبله؛ دایره‌ای به محیط ۱۶ رسم کرده و با استفاده از قضیه وارون فیثاغورس تمام ۴ بلندگوی قبلی رو طبق شکل با ۸ بلندگوی جدید با فاصله‌های دوتایی روی دایره‌ی بزرگتر جایگزین می‌کنیم. مجموع صدایی که از این ۸ بلندگو شنیده می‌شه همچنان برابر π²/4 هست.

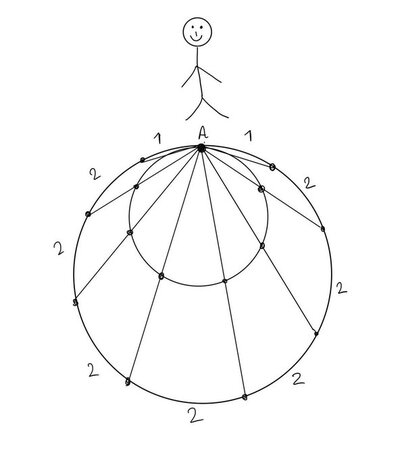
همین ایده رو برای مراحل بالاتر هم تکرار می‌کنیم؛ یعنی دایره‌های بزرگتر رو رسم و بلندگوهای جدید اضافه می‌کنیم. مجموع صدا همچنان π²/4 هست. می‌دونیم دایره‌ای که قطرش به سمت بی‌نهایت میل ‌کنه، ‌تبدیل به خط اعداد حقیقی (ℝ) می‌شه. اما در بی‌نهایت بلندگوها کجا قرارمی‌گیرن؟

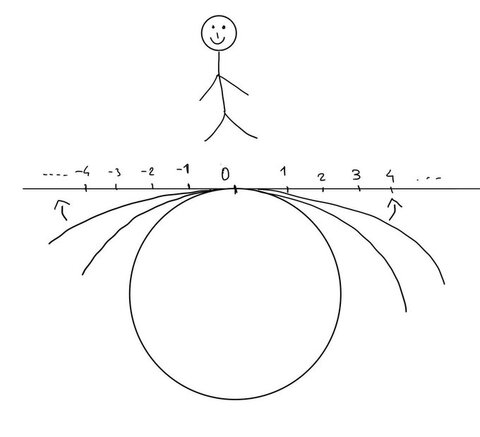
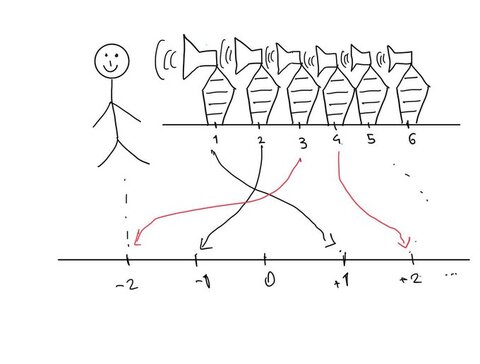
بلندگوی اول و دوم به فاصله ۱ واحد از شنونده (سمت چپ و راستش) بودن، پس روی نقاط ۱+ و ۱- قرار می‌گیرن، سومی و چهارمی به فاصله ۳، پس روی نقاط ۳+ و ۳- قرار می‌گیرن، و به همین ترتیب تا انتها. مجموع صدایی که از همه‌ی این بلندگوها شنیده می‌شه برابره با سری زیر که بعد ساده‌شدن می‌شه:

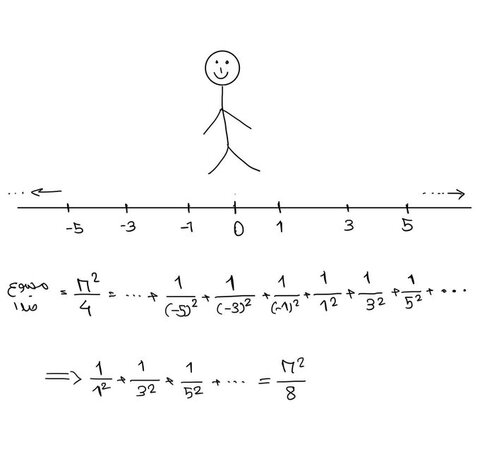
اما این سری از مسئله بازل فقط جمع عکس مجذور اعداد زوج رو کمتر داره. نحوه محاسبه سری اعداد زوج هم شبیه قبله؛ در بی‌نهایت که دایره تبدیل به خط شد، بلندگوها روی اعداد مثبت و منفی زوج می‌شینن. چون اولین بلندگو به فاصله‌ی ۲ از شنونده‌ست، جمع این سری باید ۱/۴ برابر مسئله بازل باشه.

چون جمع سری عکس مجذور اعداد زوج و فرد باید برابر با مسئله بازل باشه، نتیجه می‌گیریم جمع عکس مجذور اعداد فرد که پیش‌تر محاسبه کردیم باید ۳/۴ برابر مسئله بازل باشه؛ که یعنی ۳/۴ ضرب‌در π²/8 که می‌شه همون π²/6 معروف!