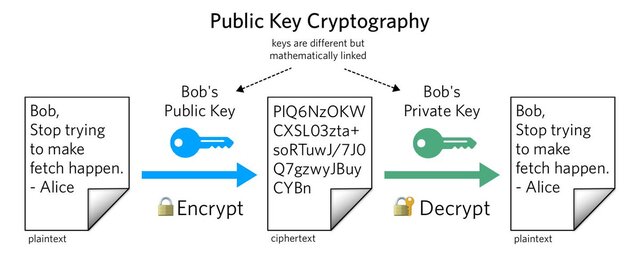
اگر از ارزهای مجازی و خصوصاً بیتکوین استفاده کرده باشین حتماً می‌دونید که ارز در کیف پول اینترنتیتون ذخیره می‌شه. هر کیف پول یه آدرس عمومی داره (Public Key). تا حالا به این فکر کردین که این آدرس عجیب و غریب‌ چجوری ساخته می‌شه و منطقش چیه؟

نکته‌ی جالب‌تر اینه که کلید عمومی هر شخص مستقیماً از کلید خصوصیش (Private Key) تولید می‌شه! اما بیتکوین چجوری امنیتش رو تضمین می‌کنه؟ چرا نمی‌شه با داشتن کلید عمومی به کلید خصوصی رسید؟ پاسخش در علم ریاضی نهفته‌س و قراره در ادامه با زبان ساده به همه‌ی این سوال‌ها پاسخ بدم.

کار رو با معرفی یک سری موجودات جالب در ریاضی شروع می‌کنیم؛ خم‌های بیضوی. این مبحث یکی از پیچیده‌ترین بخش‌های ریاضیه که برای درکش باید به مفاهیم گوناگونی مثل گروه‌ها و حلقه‌ها، توپولوژی، گونای خم، واریته‌های آفین، گروه‌های پیکارد و گالوا و چندتا چیز دیگه تسلط کامل داشته باشید!

تاکید کنم تعریفی که ارائه می‌دم نادقیق, سطحی و ساده‌سازی‌شده برای فهم همه‌س. به راحت‌ترین شکل ممکن، این خم‌های بیضوی رو می‌شه مجموعه‌ای از نقاط در صفحه‌ی ℝ² در نظر گرفت که با رابطه‌ی زیر مشخص می‌شن:

\[y^2=x^3+ax+b\]

هر زوج مرتب (x,y) که تو رابطه‌ی بالا صدق کنه عضوی از این خم هست.

نکته‌ی اساسی که این رابطه رو از سایر روابط رایج در صفحه جدا می‌کنه اینه که مجموعه‌ی همه نقاطی که عضو خم‌های بیضوی هستن علاوه بر ویژگی‌های خاص هندسی، یه ساختار بسیار زیبای جبری هم دارن؛ ساختار حبری رو به طور غیردقیق مجموعه‌ای از روابط و اعمال جبری روی نقاط این خم در نظر بگیریم.

پس می‌شه بین نقاط این خم یه عمل جمع دلخواه با عضو وارون و قرینه‌ی جمعی تعریف کرد و مطمئن بود این مجموعه نقاط نسبت به عمل جمع بسته هستن؛ یعنی هر جمع دلخواه از نقاط دوباره یه نقطه جدید روی خم می‌شن. علت این که می‌شه چنین جمعی رو تعریف کرد به ویژگی جالبی توی این خم‌ها بر می‌گرده.

می‌شه به طور صریح ثابت کرد که اگر بین هر دونقطه‌ی دلخواه‌ روی نمودار خم بیضوی خطی رسم کنیم، این خط حتماً نمودار رو در یک و تنها یک نقطه‌ی دیگه قطع می‌کنه. چون این ویژگی برای هر جفت نقطه صادقه، عمل جمع رو به دلایل خاصی قرینه‌ی اون نقطه‌ی سوم نسبت به محور xها تعریف می‌کنیم.

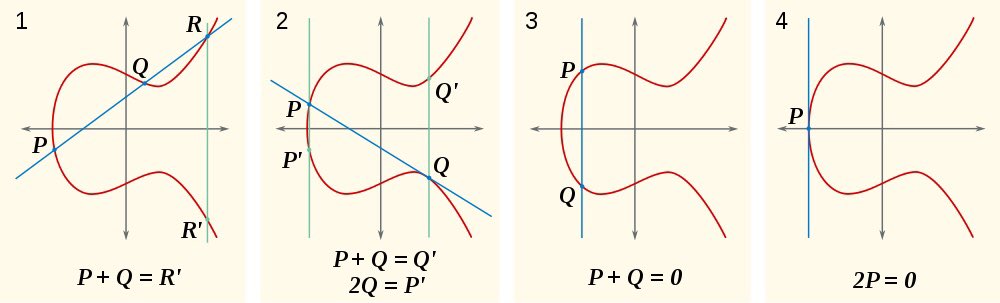
ا داشتن مختصات دو نقطه، فرمول نقطه‌ی سوم صریحاً به دست میاد. برای جمع یک نقطه با خودش از خط مماس بر اون نقطه استفاده می‌کنیم. مهم‌ترین ویژگی این جمع اینه که برگشت‌ناپذیره؛ یعنی اگر برای نقطه‌ی معلوم P و عدد نامعلوم n مقدار n×P رو بدونیم، خود n به هیچ‌وجه قابل‌محاسبه نیست.

برگشت‌پذیری در اعداد حقیقی به علت وجود عمل تقسیم برقراره ولی در خم‌های بیضوی صادق نیست. این حقیقت هم از لحاظ جبری قابل‌اثباته و هم به طور هندسی می‌شه فهمیدش. مشخصه که اگر مقدار n×P رو در نمودار به ما بدن به هیچ‌وجه نمی‌شه پی برد که نقطه‌ی P چند بار در صفحه با خودش جمع شده.

نکته‌ی مهم دیگه در مورد خم‌های بیضوی اینه که می‌شه روی میدان دیگری جز اعداد حقیقی هم تعریفشون کرد. مثلاً اگر میدان ورودی ما اعداد گویا یا حتی مختلط باشن، نقاطی با مختصات گویا و مختلط وجود دارن که عضو خم هستن و همه‌ی ویژگی‌های جبری و هندسی فوق از جمله عمل جمع براشون صادقه.

از میدان‌های مهمی که می‌شه خم‌های بیضوی رو روشون تعریف کرد میدان‌های متناهی Fp هستن. این میدان‌ها تنها شامل p عضون؛ از عدد 0 تا p-1. منطق جمع نقاط توی این میدان‌ها به این صورته که حاصل‌جمع هر دو نقطه برابره با باقی‌مانده اون حاصل بر عدد p که دوباره یکی از اعداد 0 تا p-1 هست.

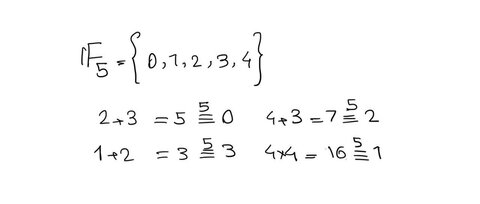
با این مقدمه بریم سراغ اصل کار. بیتکوین برای ساخت کلیدهاش از یک خم بیضوی خاص به نام Secp256k1 استفاده می‌کنه که معادله‌ش اینه:

\[y^2=x^3+7\]

این خم روی میدان متناهی Fp تعریف می‌شه که p یک عدد اول و برابره با:

\[p=2^{256}-2^{32}-977\]

این عدد ۷۷رقمی یکی از بزرگترین اعداد اول شناخته‌شده‌ست.

زمانی که کیف پول رو می‌سازید یک کلید خصوصی به اون نسبت داده می‌شه. این کلید خصوصی در حقیقت یک عدد بسیار بزرگه که ابتدا به مبنای ۱۶ (Hex) منتقل شده و در آخر تبدیل به آدرس ظاهرشده برای شما طبق شکل زیر می‌شه (Hash). گفتیم کلید عمومی از روی همین کلید خصوصی ساخته می‌شه. اما چجوری؟

بیتکوین یک نقطه‌ی فیکس G برای همه‌ی کیف‌پول‌ها در نظر می‌گیره که مختصاتش طبق شکل زیره. برای هر کیف پول، این نقطه‌ی G دقیقاً به تعداد کلید خصوصی (Pr) بار در خودش ضرب می‌شه و کلید عمومی تولید می‌شه (Pu). طبق توضیحات چون این عمل برگشت‌ناپذیره، کلید خصوصی شما امن باقی می‌مونه!

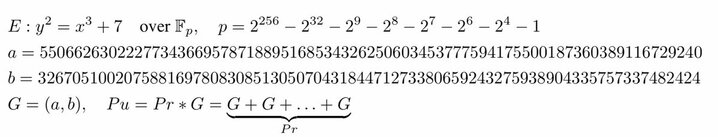
نحوه‌ی ساخت کلید عمومی هم دقیقاً مشابهه؛ ابتدا دو مولفه‌ی x و y مختصات نقطه‌ی Pu که از فرمول قبل محاسبه شد به ترتیب کنار هم گذاشته می‌شه تا ۱ عدد به دست بیاد، بعد اون عدد به مبنای ۱۶ می‌ره (حتماً هم ۶۴ رقم داره)، و در انتها هم آدرسی که برای شما نمایش داده می‌شه؛ راحت و ایمن!

حوزه‌ی تخصصی من و موضوع پایان‌نامه ارشدم رمزنگاری‌هاییه که طبق خم‌های بیضوی انجام می‌شن (Elliptic curve cryptography). من دارم در حال حاضر روی نوع خاصی از خم‌های بیضوی ( Supersingular EC’s) و نگاشت‌های بینشون کار می‌کنم و امیدوارم بشه در این راه کارهای مفیدی انجام داد.