هاروارد-امآیتی ۱. سه سوال از تورنمنت هاروارد-امآیتی ۲۰۰۸
- کوچکترین عدد صحیح مثبت n که دو رقم سمت راست آن با دو رقم سمت راست 107n برابر باشه چنده؟
- مجموع اعضای چند تا از زیرمجموعههای {2,1,...,63} برابر با ۲۰۰۸ ه؟
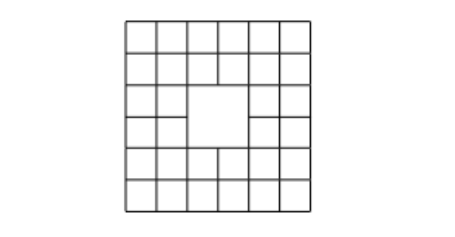
- در شکل زیر چند مستطیل (با مساحت ناصفر) وجود دارد که اضلاع آن کاملا روی خطوط قرار بگیرد؟
لینک توویتر:
سوال ۱. برای اینکه دو رقم راست دو عدد یکی باشند، باید باقیمانده هر دو بر ۱۰۰ برابر باشد. پس:
$$ \begin{aligned} 107n \equiv n\ (\textrm{mod}\ 100) &\implies \\ 7n \equiv n\ (\textrm{mod}\ 100) &\implies \\ 6n \equiv 0\ (\textrm{mod}\ 100) & \end{aligned} $$
و کوچکترین عدد مثبتی که باقیماندهی ۶ برابر آن بر ۱۰۰ صفر باشد، ۵۰ است.
سوال ۲. مجموع ۱ تا ۶۳ برابر است با $63*64/2 = 2016$. یه زیرمجموعه با مجموع ۲۰۰۸، شامل همهی اعداد به غیر از تعدادی که مجموعشون ۸ ه است. پس کافیه تعداد زیرمجموعههایی که مجموعشون ۸ میشه رو بشمریم.
- یک عضوی: $\{8\}$
- دو عضوی: $\{1,7\}$ ، $\{2,6\}$ ، $\{3,5\}$
- سه عضوی: $\{1,2,5\}$ ، $\{1,3,4\}$
پس پاسخ برابر است با ۶.
سوال ۳. با انتخاب ۲ ضلع عمودی و ۲ ضلع افقی میتوان یک مستطیل ساخت. پس تعداد کل مستطیلها، صرفنظر از اینکه ضلعی از نقطهی مرکزی میگذرد یا نه، برابر است با ${7 \choose 2}{7 \choose 2} = 21 . 21 = 441$.
اگر یکی از ضلعهای افقی مستطیل از نقطهی مرکزی بگذرد، برای دیگر ضلع افقی ۶ انتخاب داریم، و برای ۲ ضلع عمودی به طوری که نقطهی مرکز شامل روی ضلع مستطیل بیفتد، ۱۵ انتخاب. پس $15 * 6=90$ حالت داریم که یکی از ضلعهای افقی از نقطهی مرکز رد شود.
به طور مشابه ۹۰ حالت داریم که یکی از ضلعهای عمودی از نقطهی مرکز رد شود.
برای اینکه هم یک ضلع افقی و هم یک ضلع عمودی همزمان از نقطهی مرکزی رد شوند، یکی از گوشههای مستطیل باید در نقطهی مرکز باشد. پس تعداد این حالتها هم برابر است با تعداد حالتهایی که گوشهی روبرو رو بتوانیم انتخاب کنیم، یعنی ۳۶ حالت.
پس پاسخ نهایی برابر است با $441 - 2 * 90 + 36 = 297$.