پاسخ صحیح برای مسئله برابر است با 58501.2. همچنین پاسخ مسئله تکمیلی برابر است با 90.36

در هر لحظه از زمان، تنها عاملی که مشخص می‌کند به صورت میانگین چند مرحله لازم است تا اعداد روی جعبه ها به صورت مطلوب در بیاید این هست که عدد نوشته شده روی چند جعبه با عدد مطلوب نهایی برابر است. در ابتدا چون همه اعداد برابر با یک هست این میزان برابر با ۱ است. زیرا تنها عدد نوشته شده روی یک جعبه (جعبه اول) با عدد مطلوب نهایی یکسان است.

به این صورت مسئله را می‌توان با یک مدل گراف تعریف کرد: یک گراف ۷ راسی داریم که راس شماره i نماینده تمام حالاتی هست که در آن i جعبه عدد مطلوب را دارند.

در ابتدا یک نشانه بر روی راس شماره ۱ قرار دارد. در هر مرحله این نشانه بر اساس احتمالات مشخص به یکی از رئوس گراف (از جمله راس کنونی) حرکت می‌کند.

به صورت میانگین چند مرحله طول می‌کشد که نشانه به راس شماره ۶ برسد؟

در شکل می‌توانید احتمال حرکت از هر راس به رئوس دیگه را مشاهده کنید:

چنین مسائلی را می‌توان به صورت یک دستگاه معادلاتی حل کرد. در این دستگاه به ازای هر راس i یک متغیر v_i وجود دارد که پاسخ مسئله برای آن راس را نشان می‌دهد.

دستگاه معادلات مربوط به مسئله ما برابر است با:

$$ \begin{aligned} &v_0 = 1 + \frac{5}{6}v_0 + \frac{1}{6}v_1 \\ &v_1 = 1 + \frac{5}{36}v_0 + \frac{13}{18}v_1 + \frac{5}{36}v_2 \\ &v_2 = 1 + \frac{5}{18}v_1 + \frac{11}{18}v_2 + \frac{1}{9}v_3 \\ &v_3 = 1 + \frac{5}{12}v_2 + \frac{1}{2}v_3 + \frac{1}{12}v_4 \\ &v_4 = 1 + \frac{5}{9}v_3 + \frac{7}{18}v_4 + \frac{1}{18}v_5 \\ &v_5 = 1 + \frac{25}{36}v_4 + \frac{5}{18}v_5 + \frac{1}{36}v_6 \\ &v_6 = 0 \end{aligned} $$

پاسخ این دستگاه معادلاتی به صورت زیر است:

$$ \begin{aligned} &v_0 = 58507.2 \\ &v_1 = 58501.2 \\ &v_2 = 58488 \\ &v_3 = 58446 \\ &v_4 = 58224 \\ &v_5 = 55986 \\ &v_6 = 0 \end{aligned} $$

چون در ابتدا از راس شماره ۱ شروع می‌کنیم پس پاسخ مسئله برابر است با 58501.2.

با همین روش می‌توان مسئله امتیازی را هم حل کرد. اما گراف به دست آماده اندکی بزرگتر است و به این دلیل حل سوال نیاز به برنامه نویسی دارد.

در این مورد عاملی که مشخص می‌کند به طور میانگین چند گام باقیمانده، این است که از هر عدد مجزا چندتا داریم. دقت کنید که خود عددها و ترتیبشان مهم نیست و فقط سایز دسته‌ها مهمه. مثلا اگر روی جعبه‌ها نوشته شده باشد ۱ ۳ ۱ ۵ ۵ ۲، این حالت عبارت است از (2,2,1,1) زیرا ۴ عدد مجزا روی جعبه‌ها نوشته شده که از ۲ تا ۲ بار نوشته شده و از ۲ تا یک بار. همچنین اگر روی جعبه‌ها نوشته شده بود ۶ ۶ ۱ ۲ ۴ ۴ باز هم حالتمان میشد همان (2,2,1,1) با اینکه اعداد متفاوت از مثال قبل است. ولی سایز دسته‌های عددهای مجزا مثل مثال قبل است.

در ابتدا عدد نوشته شده روی ۶ جعبه یکسان است، پس از حالت (6) شروع می‌کنیم. هدف این است که به حالت (1,1,1,1,1,1) برویم که نمایانگر این است که ۶ عدد متفاوت روی ۶ جعبه نوشته شده.

این حالت‌های مختلف رو به شکل زیر نامگذاری می‌کنیم:

$$ \begin{aligned} v_0&=(6)\\ v_1&=(5,1)\\ v_2&=(4,2)\\ v_3&=(3,3)\\ v_4&=(4,1,1)\\ v_5&=(3,2,1)\\ v_6&=(2,2,2)\\ v_7&=(3,1,1,1)\\ v_8&=(2,2,1,1)\\ v_9&=(2,1,1,1,1)\\ v_{10}&=(1,1,1,1,1,1) \end{aligned} $$

در زیر گراف مسئله و دستگاه معادلاتی و پاسخ آن را آورده ایم:

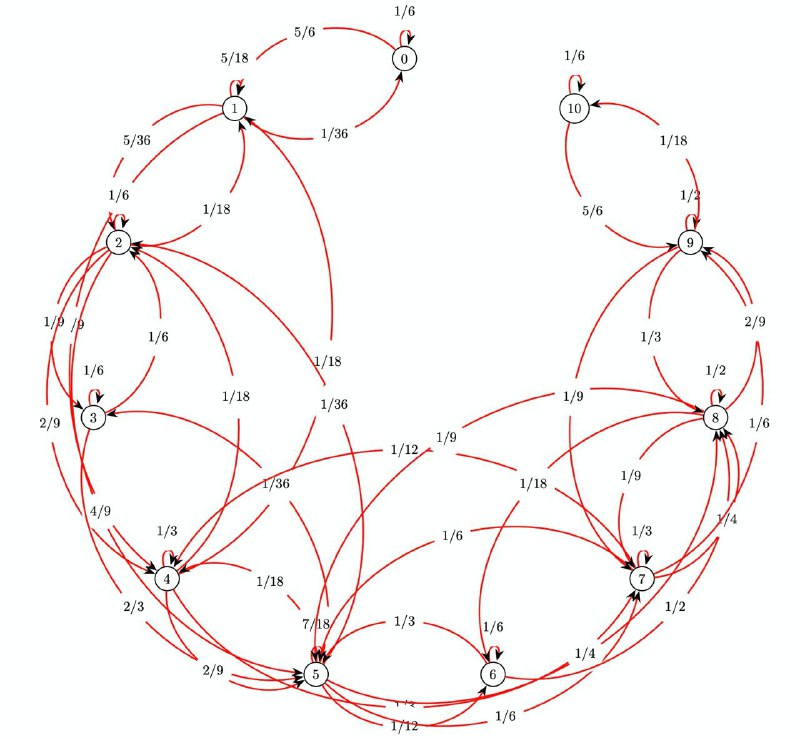
$$ \begin{aligned} &v_0 = 1 + \frac{1}{6}v_0 + \frac{5}{6}v_1 \\ &v_1 = 1 + \frac{1}{36}v_0 + \frac{5}{18}v_1 + \frac{5}{36}v_2 + \frac{5}{9}v_4 \\ &v_2 = 1 + \frac{1}{18}v_1 + \frac{1}{6}v_2 + \frac{1}{9}v_3 + \frac{2}{9}v_4 + \frac{4}{9}v_5 \\ &v_3 = 1 + \frac{1}{6}v_2 + \frac{1}{6}v_3 + \frac{2}{3}v_5 \\ &v_4 = 1 + \frac{1}{18}v_1 + \frac{1}{18}v_2 + \frac{1}{3}v_4 + \frac{2}{9}v_5 + \frac{1}{3}v_7 \\ &v_5 = 1 + \frac{1}{36}v_2 + \frac{1}{36}v_3 + \frac{1}{18}v_4 + \frac{7}{18}v_5 + \frac{1}{12}v_6 + \frac{1}{6}v_7 + \frac{1}{4}v_8 \\ &v_6 = 1 + \frac{1}{3}v_5 + \frac{1}{6}v_6 + \frac{1}{2}v_8 \\ &v_7 = 1 + \frac{1}{12}v_4 + \frac{1}{6}v_5 + \frac{1}{3}v_7 + \frac{1}{4}v_8 + \frac{1}{6}v_9 \\ &v_8 = 1 + \frac{1}{9}v_5 + \frac{1}{18}v_6 + \frac{1}{9}v_7 + \frac{1}{2}v_8 + \frac{2}{9}v_9 \\ &v_9 = 1 + \frac{1}{9}v_7 + \frac{1}{3}v_8 + \frac{1}{2}v_9 + \frac{1}{18}v_{10} \\ &v_{10} = 0 \end{aligned} $$

که حل دستگاه معادلات بالا میشود:

$$ \begin{aligned} v_0 &= 90.36 \\ v_1 &= 89.16 \\ v_2 &= 88.44 \\ v_3 &= 88.2 \\ v_4 &= 87.48 \\ v_5 &= 86.64 \\ v_6 &= 86.04 \\ v_7 &= 84.6 \\ v_8 &= 83.64 \\ v_9 &= 76.56 \\ v_{10} &= 0 \end{aligned} $$

و پاسخ مسئله برابر است با 90.36.