یافتن مساحت ۲
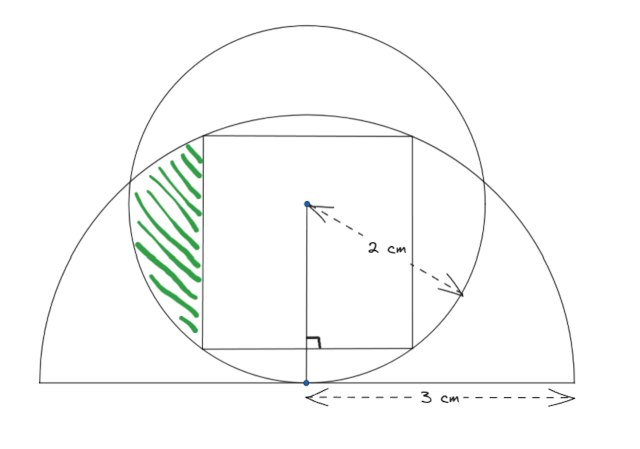
در شکل زیر یک دایره به شعاع ۲ مماس بر مرکز ضلع نیمدایرهای به شعاع ۳ قرار گرفته، و مربعی در اشتراک آنها محاط شده.
مساحت بخشی که با هاشور سبز مشخص شده چند است؟
راهحل 1
پاسخ تقریبا برابر است با ۱٫۳۴۹.
ابتدا طول ضلع مربع را حساب میکنیم. اگر مرکز نیمدایره را مبدا مختصات در نظر بگیریم، در این صورت اگر ضلع سمت راست مربع در طول \(x_1\) قرار داشته باشد، طول ضلع افقی مربع برابر خواهد بود با \(2x_1\). طول ضلع عمودی مربع هم برابر خواهد بود با فاصله نقاط برخورد خط \(x=x_1\) با نیمدایره سبز (یعنی \((x_1,y_2)\)) و نیمهی پایین دایره قرمز (یعنی \((x_1,y_1)\)). چون ضلعهای مربع برابر است، این دو مقدار را برابر قرار میدهیم تا \(x_1\) را بدست بیاوریم.
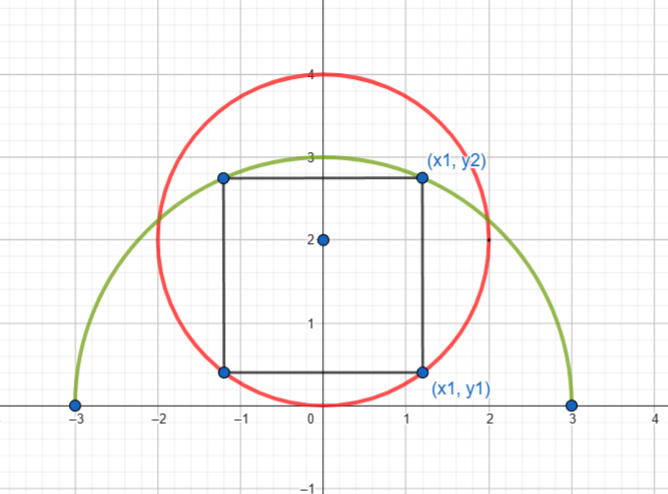
تابع نیمدایره سبز برابر است با \(y=\sqrt{9-x^2}\) و تابع نیمهی پایین دایره قرمز برابر است با \(y=2-\sqrt{4-x^2}\). پس طول ضلع عمودی مربع برابر است با \(\sqrt{9-x_1^2} + \sqrt{4-x_1^2} - 2\). اگر این طول را برابر با طول ضلع افقی (یعنی \(2x_1\)) قرار دهیم و حل کنیم، مقدار \(x_1\) تقریبا برابر خواهد شد با 1.18411 و بنابراین ضلع مربع تقریبا برابر خواهد بود با 2.36822. برای حل این معادله از WolframAlpha استفاده کردیم.
اکنون به مساحت بخشهای مشخص شده با هاشور سبز و هاشور قرمز در شکل زیر میپردازیم. بخش قرمز قطعهای از دایره است، و بخش آبی قطعهای از نیمدایره. با توجه به اینکه وتر هر دو مساوی با ضلع مربع است، و با داشتن شعاع هر دو، میتوان زاویه روبروی هر کدام را حساب کرد.
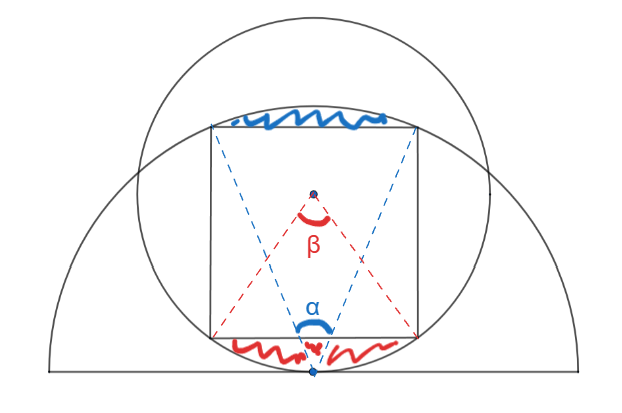
$$ \begin{aligned} \beta &= 2 \arcsin\left(\frac{1.18411}{2}\right) \approx 1.26721 \text{ rad} \\ \alpha &= 2 \arcsin\left(\frac{1.18411}{3}\right) \approx 0.81149 \text{ rad} \end{aligned} $$
و سپس با استفاده از فرمول مساحت قطعه دایره (\(A=\frac{R^2}{2}(\theta - \sin \theta)\)) مساحت هر کدام را حساب کرد:
$$ \begin{aligned} \text{A(red)} &= \frac{2^2}{2}(\beta-\sin\beta) \approx 0.62588 \\ \text{A(blue)} &= \frac{3^2}{2}(\alpha-\sin\alpha) \approx 0.38779 \end{aligned} $$
برای یافتن مساحت بخش هاشور نارنجی، ابتدا عرض تقاطع دایره و نیمدایره را پیدا میکنیم، سپس با استفاده از آن زوایای \(\gamma\) و \(\theta\) را حساب میکنیم.
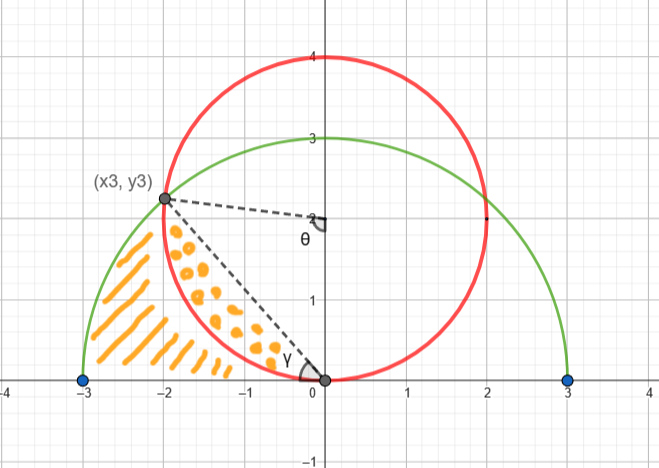
$$ \begin{align} \left. \begin{aligned} x_{3}^{2}+y_3^2&=3^2 \\ x_3^2+(y_3 - 2)^2&=2^2 \end{aligned} \right\} \quad &\implies \quad y_3 = 2.25 \\ \quad &\implies \quad \left\{ \begin{aligned} \theta &= \arcsin\left(\frac{2.25-2}{2}\right) + \frac{\pi}{2} \approx 1.69612 \text{ rad} \\ \gamma &= \arcsin\left(\frac{2.25}{3}\right) \approx 0.84806 \text{ rad} \end{aligned} \right. \end{align} $$
مساحت هاشور نارنجی + خالخالی نارنجی میشود: \(0.5 \times \gamma \times 3^2 \approx 3.81628 \).
مساحت خالخالی نارنجی با استفاده از فرمول مساحت قطعه دایره میشود: \(\frac{2^2}{2}(\theta-\sin\theta) \approx 1.40793\).
با تفریق ایندو مساحت هاشور نارنجی میشود تقریبا: 2.40834.
و بالاخره مساحت قسمت سبز خواسته شده در مساله اصلی برابر است با مساحت نیمدایره منهای مساحت مربع منهای مساحت هاشور قرمز منهای مساحت هاشور آبی منهای دو برابر مساحت هاشور نارنجی، تقسیم بر ۲.
که تقریبا برابر است با: ۱٫۳۴۹.
راهحل 2
راهحل دیگری با انتگرالها وجود دارد که @fork_them پیشنهاد داد.
در گام اول مثل راهحل قبل، ضلع مربع را پیدا میکنیم که میشود تقریبا 2.36822 و مولفهی x ضلع سمت چپ مربع میشود \(x_4 \approx -1.18411\).
در گام دوم تقاطع دایرهی قرمز و نیمدایرهی سبز رو پیدا میکنیم. در راهحل قبل یافتیم که \(y_3 = 2.25\). اکنون با قرار دادن آن در فرمول نیمدایره \(x_3\) را بدست میآوریم:
$$ x_3^2+y_3^2 = 3^2 \quad \implies \quad x_3 \approx -1.98431 $$
اکنون اگر منطقه مورد نظر را به دقت نگاه کنیم، میتوان آنرا به ۳ بخش تقسیم کرد:
- بخش سبز که بین نیمدایره سبز و خط \(x=2\) قرار دارد
- بخش قرمز که بین خط \(x=2\) و نیمهی پایین دایرهی قرمز قرار دار.
- بخش آبی که بین نیمهی بالای دایرهی قرمز و خط \(x=2\) قرار دارد.
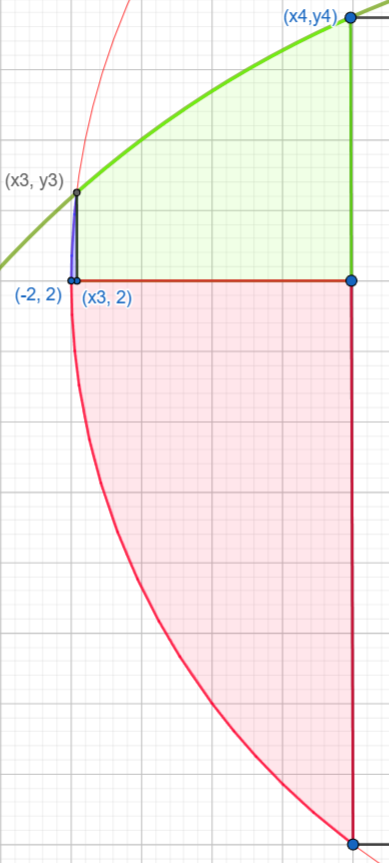
اکنون مساحت هر کدام از بخشها را با انتگرال بدست میآوریم:
$$ \begin{aligned} A(blue) &= \int_{-2}^{x_3}\sqrt{4-x^2}dx \approx 0.00262 \\ A(green) &= \int_{x_3}^{x_4}(\sqrt{9-x^2}-2) dx \approx 0.42644 \\ A(red) &= \int_{-2}^{x_4}2 - (-\sqrt{4-x^2} + 2) dx \approx 0.92011 \end{aligned} $$
که با جمع کردن سه مقدار بالا پاسخ مساله تقریبا ۱٫۳۴۹ به دست میآید.