پاسخ درست برابر است با:

$$ ({40 \choose 25} - {40 \choose 26}) \times 25! \times 15! $$

فرض کنید m نفر اسکناس 5$ و n نفر اسکناس 10$ داشته باشن. حالت یک صف رو با نموداری مثل زیر نشون میدیم که از مبدا شروع می‌کنیم و اگه نفر بعدی 5$ بود، بالا راست میریم و اگه 10$ بود پایین راست.

برای اینکه نمودارها خیلی بزرگ نشود، به جای ۲۵ و ۱۵ مساله اصلی در نمودارهای زیر m رو ۶ و n رو ۴ در نظر گرفتیم. ولی ایده کلی همان است.

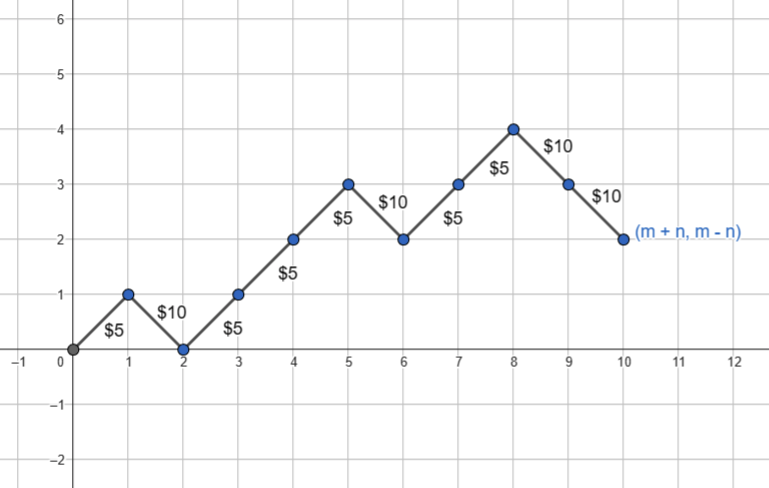
تعداد اینچنین نمودارهایی \({n+m \choose m}\) خواهد بود.

دقت کنید که در هر لحظه مختصات y نمودار نشانگر تعداد ۵ دلاری‌ها در صندوقه، پس حالت‌های غیر مجاز حالت‌هایی هستند که نمودار پایین‌تر از محور y می‌شود. مثل حالت زیر:

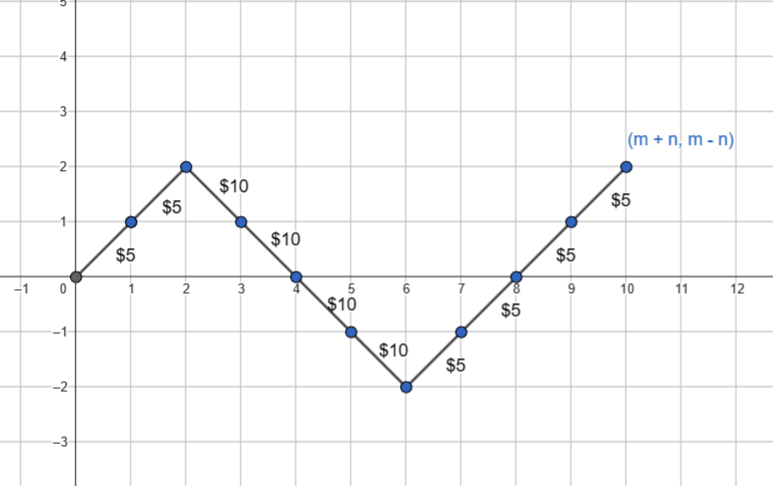
برای شمردن این حالات غیر مجاز، به این دقت می‌کنیم که این حالت‌ها حالت‌هایی هستند که نمودار با خط y=-1 برخورد می‌کند.

برای همچنین حالتی، می‌توان یک حالت متناظر ساخت که در آن ماقبل اولین برخورد با y=-1 را نسبت به y=-1 قرینه کرده‌ایم. مثلا برای نمودار بالا:

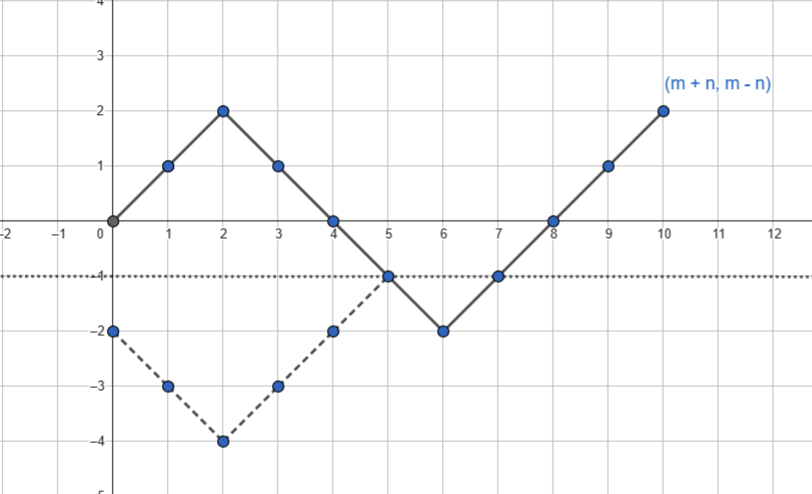
چنین نمودارهایی از (2-, 0) شروع می‌شوند و مثل حالت قبل در (m+n, m-n) تمام می‌شوند. این نمودارها با حالات غیر مجاز تناظر یک به یک دارند.

با حل ۲ معادله دو مجهولی، می‌توان نشان داد که در این نمودارهای قرینه تعداد حرکت به بالا راست‌ها برابر است با m+1. پس تعداد این نمودارها برابر است با \({n+m \choose m+1}\).

پس تعداد کل تعداد نمودارهای مجاز برابر می‌شود با \({n+m \choose m} - {n+m \choose m+1}\). در این نمودارها بین افراد تمایز قائل نشدیم. اگر افراد را متمایز در نظر بگیریم، جواب مساله اصلی می‌شود

$$ ({n+m \choose m} - {n+m \choose m+1}) \times n! \times m! $$