پاسخ مورد نظر ۷ می‌باشد.

چون با هر پرسش فضای جستجو را به دو بخش می‌کنیم، پاسخ کمتر از ⌈log₂ 121⌉=7 نمی‌تواند باشد.

ابتدا یک راه‌حل ساده با ۸ حرکت را توضیح می‌دهیم و سپس به توضیح ۷ حرکت می‌پردازیم.

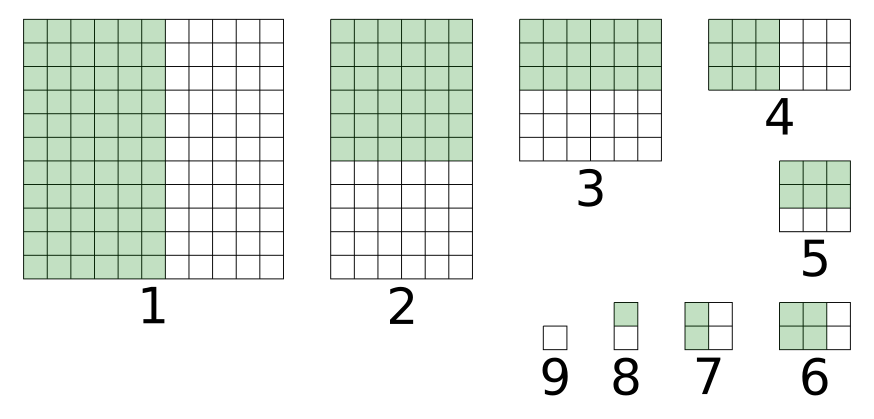
اگر با الهام از باینری‌سرچ مستطیل اصلی را هر دفعه به ۲ مستطیل تقریبا مساوی تقسیم کنیم و یکی از آن دو رو بپرسیم، در حداکثر ۸ حرکت به جواب می‌رسیم: سوال اول مستطیل 11x6، سپس 6x6، سپس 3x6، سپس 3x3، سپس 3x2، سپس 2x2، سپس 2x1، و بالاخره 1x1. در شکل زیر فضای بزرگترین جستجوی باقیمانده در هر مرحله (مستطیل نشان‌داده شده) و پرسش آن (بخش سبز) نشان داده شده.

برای اینکه به ۷ حرکت برسیم، به ۲ نکته‌ی کلیدی توجه می‌کنیم:

• پس از حرکت اول باید حداکثر ۶۴ خانه در فضای جستجو باقی مانده باشد، پس از حرکت دوم حداکثر ۳۲، ... و پس از حرکت هفت یک. در راه‌حل بالا پس از حرکت اول ممکن بود ۶۶ خانه باقی مانده باشد.
• لزومی ندارد فضای جستجوی باقیمانده مستطیل پیوسته باشد!

با در نظر گرفتن نکات بالا احتمالا خودتان بتوانید روی کاغذ یک سری راه‌حل پیدا کنید.

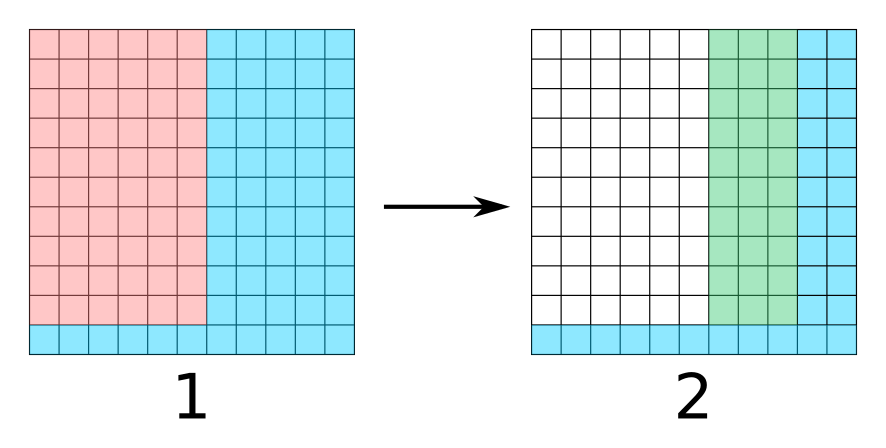
یک راه (شبیه راه‌حل _peyman_m) این است که مثل شکل ۱ ابتدا مستطیل قرمز را بپرسیم. جواب آری را بعدا بررسی خواهیم کرد، ولی اگر جواب نه بود، مستطیل سبز شکل ۲ را می‌پرسیم.

در این ۲ سوال فضای جستجو را حرکت اول به حداکثر ۶۱ و حرکت دوم حداکثر ۳۱ خانه محدود کردیم.

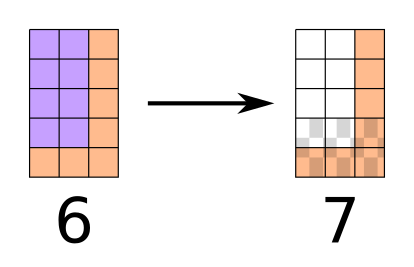
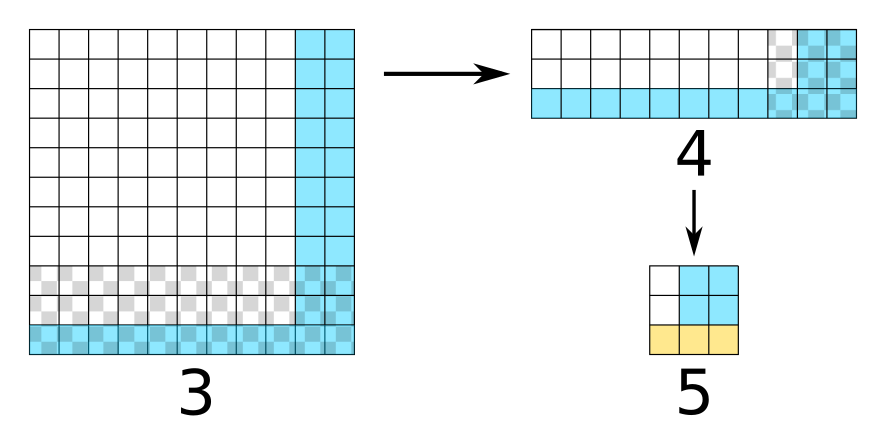
جواب آری شکل ۲ را بعدا بررسی خواهیم کرد، ولی اگر جواب نه بود، ۳۱ خانه باقی می‌ماند. پرسیدن بخش شطرنجی شکل ۳ فضای جستجو را به ۲ بخش ۱۵ خانه و ۱۶ خانه تقسیم می‌کند. بخش ۱۶ خانه چون هر دو ضلعش توان ۲ است، در ۴ مرحله می‌توان به مستطیل‌های کوچکتر مساوی تقسیم کرد و پرسید. بخش ۱۵ تایی در شکل ۴ نشان داده شده، که بخش شطرنجی مشخص شده را سوال می‌کنیم. پس از این پرسش هر ۲ حالت آری و نه را می‌توان با حداکثر ۳ سوال دیگر به یک خانه رساند. که در مجموع حداکثر ۷ پرسش می‌شود.

تکلیف مستطیل قرمز شکل یک و مستطیل سبز شکل دو باقی مانده است. مستطیل قرمز را با ۲ پرسش و مستطیل سبز را با یک پرسش می‌توان به مستطیل 3x5 تقلیل داد. دو سوال اول این حالت در شکل‌های ۶ و ۷ مشخص شده، که بعد از آن به آسانی با ۲ سوال دیگر می‌توان به یک خانه رسید.