پاسخ دقیق سوال برای n نقطه برابر است با \(\frac{1}{n^2}\).

چون در صورت سوال جواب تقریبی خواسته بودیم، در ادامه یک راه‌حل ساده و بدون استفاده از انتگرال ارائه می‌دهیم که یک جواب با تقریب دو به ما میدهد.

از روش دو گونه شماری برای به دست آوردن پاسخ استفاده میکنیم. فرض کنید پاسخ سوال (فاصله میانگین برای نزدیک ترین دو نقطه از n نقطه تصادفی بر دایره) برابر باشد با f(n).

می‌خواهیم احتمال اینکه با اضافه کردن یک نقطه n+1 ام فاصله نزدیک ترین دو نقطه تغییر کند را محاسبه کنیم.

این احتمال بین n*f(n) و 2n*f(n) است.

برای دیدن این موضوع، فرض کنید برای یک آرایش خاص A فاصله دو نقطه نزدیک‌ترین برابر با f(n,A) باشد. به ازای هر یک از n نقطه، کمانی از دایره که فاصله آن از آن نقطه برابر با f(n,A) باشد را رنگی میکنیم. قسمت سمت پادساعتگرد آن کمان را با آبی و قسمت سمت ساعتگرد آن را با قرمز. چون f(n,A) برابر با فاصله نزدیک ترین دو‌نقطه است پس تمام کمان های آبی مجزا هستند همچنین تمام کمان های قرمز هم مجزا هستند. هرچند کمان های قرمز و آبی میتوانند اشتراک داشته باشند پس اندازه همه کمان‌های رنگی عددیست بین n*f(n,A) و 2n*f(n,A).

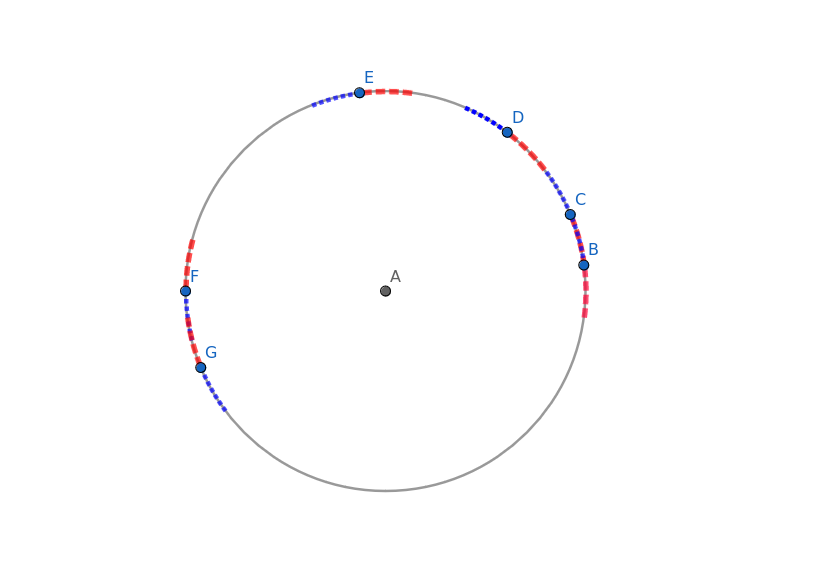
پس با توجه به اینکه محیط دایره ۱ است، در صورت اضافه کردن نقطه n+1 ام، احتمال این که بر روی یک کمان رنگی قرار گیرد عددیست بین n*f(n,A) و 2n*f(n,A).

اگر میانگین این احتمال را برای همه آرایش‌های n نقطه اول حساب کنیم این احتمال عددیست بین n*f(n) و 2n*f(n).

حال به صورت دیگری این احتمال را حساب میکنیم چون همه n+1 نقطه گذاشته شده بر روی دایره تصادفی هستند، پس‌ احتمال این که هر نقطه ای یکی از دو سر نزدیک ترین دو نقطه باشد برابر است با \(2/(n+1)\).

پس داریم:

$$ \begin{align} \left. \begin{aligned} 2/(n+1) >= n\times f(n) \\ 2/(n+1) <= 2n\times f(n) \end{aligned} \right\} \quad &\implies \quad \frac{1}{n\times(n+1)} <= f(n) <= \frac{2}{n\times(n+1)} \end{align} $$