هشمت و قلی
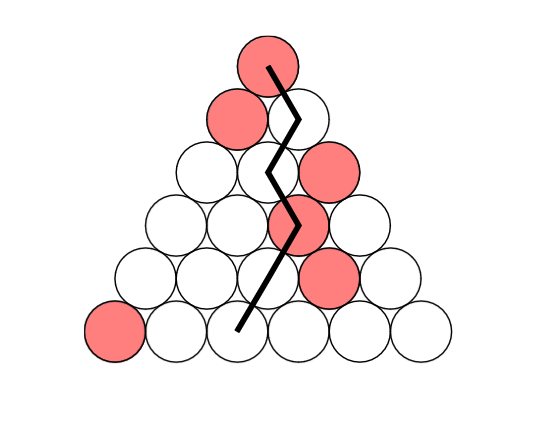
(سوال المپیاد جهانی ریاضی امسال با اندکی دخل و تصرف)
۱۳۶۹ ردیف گوی داریم که در ردیف شماره i ، i گوی قرار دارد. گوی j ام هر ردیف با گوی های j و j+1 ام ردیف بعدی در ارتباط است.
یک مسیر نینجایی تشکیل شده از ۱۳۶۹ گوی که هر کدام به یک ردیف تعلق دارند و هر گوی مسیر با گوی ردیف بعدی مسیر در ارتباط هست.
هشمت از هر ردیف یک گوی را با رنگ قرمز رنگ میکند و پس از آن قلی یک مسیر نینجایی پیدا میکند که بیشترین تعداد گوی قرمز را شامل باشد.
اگر هشمت هیچ همکاری با قلی نکند، حداقل تعداد گوی قرمز مسیر نینجایی قلی چقدر است؟
لینک مساله در توویتر: https://twitter.com/Riazi_Cafe/status/1699307153184739688
پاسخ سوال ۱۱ هست.
ما باید دو گزاره را اثبات کنیم:
گزاره اول این است که روشی برای هشمت وجود دارد که اگر به آن صورت گویها را رنگآمیزی کند، تعداد گویهای هر مسیر نینجا حداکثر ۱۱ میشود.
گزاره دوم این است که هر گونه که هشمت گوی ها را رنگ کند، مسیر نینجایی با ۱۱ گوی رنگی وجود دارد.
ابتدا گزاره اول را نشان میدهیم. شیوه رنگ کردن زیر را در نظر بگیرید:
1 ← 1
2 ← 1
3 ← 3
4 ← 1
5 ← 3
6 ← 5
7 ← 7
8 ← 1
…
به صورت کلی از هر سطر 2^i گوی شماره یک را رنگ میکنیم و به ازای هر. i﮲^2 > j => ﮲i گوی شماره 1+2*j از سطر 2^i+﮲j را رنگ میکنیم.
در این صورت از هر بازه از سطر های [1,1] [2,3] [4,7] … [512,1023] [1024,1369] حداکثر یک گوی رنگی در هر مسیر نینجا وجود خواهد داشت.
پس تعدادگوی های رنگی مسیر قلی حداکثر برابر با ۱۱ خواهد بود.
در ادامه گزاره دوم را نشان میدهیم. به عبارت دیگر نشان میدهیم به ازای هر رنگ آمیزی هشمت، مسیری نینجایی برای قلی وجود دارد که ۱۱ گوی آن رنگ شده.
برای این کار از قضیه دیلوورث استفاده میکنیم.
قضیه دیلوورث نشان میدهد که اگر به ازای یک رنگ آمیزی از گوی ها هیچ مسیر نینجایی با ۱۰ گوی رنگی وجود نداشته باشد، پس میتوان سطرهای گوی ها را به ۱۰ دسته تقسیم کرد که در هر دسته، اگر دو سطر i و j وجود دارند فاصله گوی های رنگ آنها بیشتر از |i-j| می باشد
چون ۲ به توان ۱۰ کمتر از ۱۳۶۹ هست، پس در یکی از دسته ها به ازای یک i، بیشتر از i/2 سطر با اندازه کمتر یا مساوی i قراز خواهد گرفت.
می توان مشاهده کرد که در این صورت دو سطر i و j در آن دسته قرار خواهند داشت که فاصله گوی رنگی آن ها کمتر یا مساوی |i-j| خواهد بود که با شرط گفته شده تناقض دارد.