مسالهای از ابوریحان بیرونی
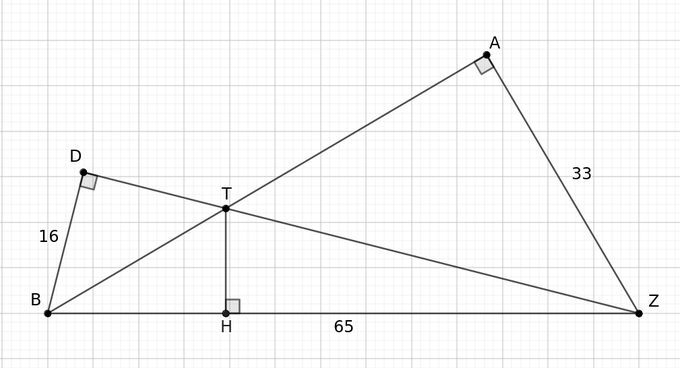
دو مثلث قائمالزاویه ABZ و DBZ و طول اضلاع آن داده شده. طول TH را پیدا کنید.
طول ZA=33
طول BD=16
طول BZ=65
لینک مساله در توویتر: https://twitter.com/Riazi_Cafe/status/1701844480939397217
راهحل 1
طبق قضیه فیثاغورث، داریم AB=56 و DZ=63. با در نظر گرفتن B به عنوان مبدا، تابع خطوط AB و DZ را مینویسیم. مختصات y محل تقاطع این دو خط برابر با جواب است.
تابع خط را میتوان با داشتن شیب و یک نقطه از آن خط نوشت. شیب خط برابر تانژانت زاویه آن با محور x در راستای مثبت است.
$$ \begin{align} \left. \begin{aligned} BA:& y = \frac{33}{56} x \\ DZ:& y = -\frac{16}{63}(x - 65) \end{aligned} \right\} \quad &\implies \quad x \approx 19.57647, y \approx 11.53613 \end{align} $$
راهحل 2
ابتدا طول BT را بدست میآوریم، و با ضرب آن در سینوس زاویه TBH حاصل را بدست میآوریم.
$$ \begin{aligned} \angle TBH &= \arcsin(\frac{33}{65}) \\ \angle DBH &= \arccos(\frac{16}{65}) \\ \angle DBT &= \angle DBH - \angle TBH \\ \\ BT &= \frac{16}{\cos(\angle DBT)} \\ \\ TH &= BT \cdot \sin(\angle TBH) \approx 11.53613 \end{aligned} $$
راهحل 3
(راهحل بیرونی)
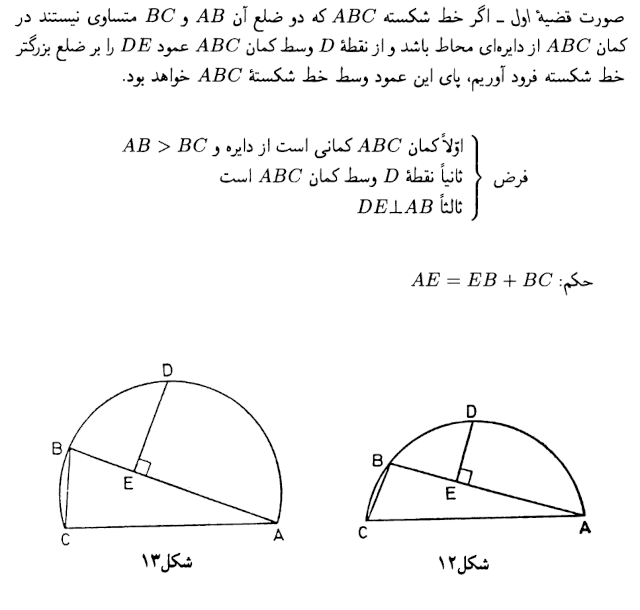
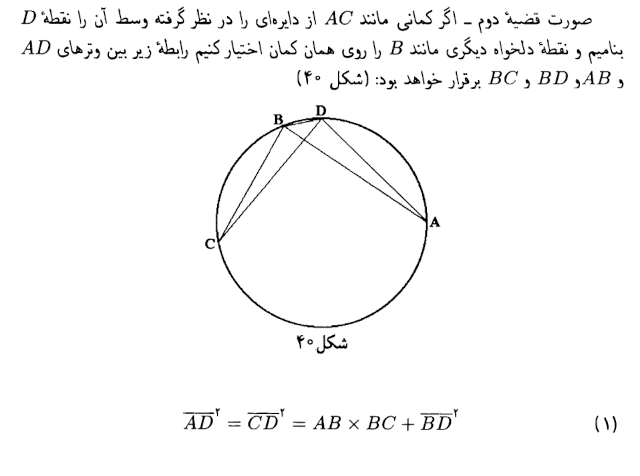
موضوع این کتاب بیرونی ۴ قضیه دربارهی وترهای دایره است و سعی کرده مسالهها رو با استفاده از ۴ قضیهای که در ابتدای کتاب آورده حل کند و دنبال سادهترین راه نبوده. پس این راهحل کمی پیچیدهتر از راهحلهای ما است.
اگر به قطر BZ دایرهای رسم کنیم به خاطر قائمالزاویه بودن دو مثلث از A و D خواهد گذشت.
همچنین در شکل زیر کمان نقطه C طوری انتخاب میشود که کمان BC با کمان AD برابر باشد.
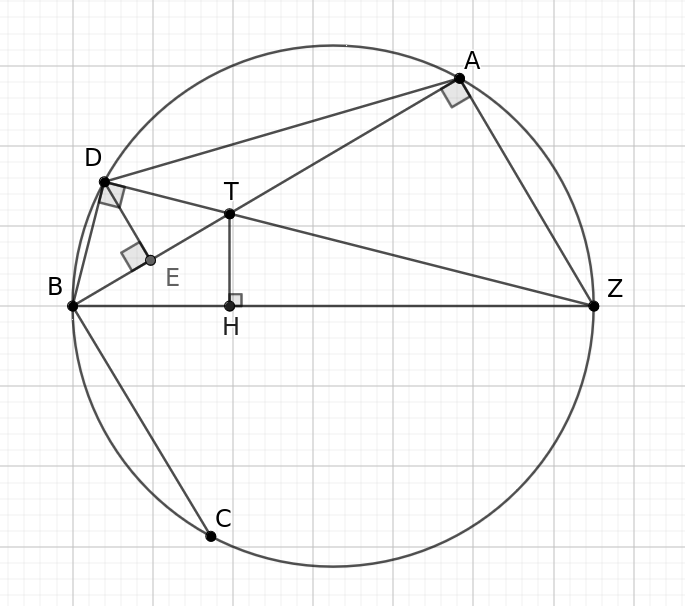
خلاصه راهحل:
- با استفاده از قضیهی بطلمیوس طول AD را بدست میآوریم.
- با استفاده از قضیه دوم کتاب بیرونی BC را بدست میآوریم.
- با استفاده از قضیه اول کتاب بیرونی، E وسط خط شکسته ABC است. چون AB و BC را داریم، پس BE و AE را میتوانیم بدست بیاوریم.
- طول DE را با استفاده از قضیهی فیثاغورث در مثلث BDE بدست میآوریم.
- با استفاده از قضیه ارتفاع وارد بر وتر در مثلث BDT طول ET را بدست میآوریم.
- با استفاده از تناسب مثلثهای TBH و AZB مقدار TH را بدست میآوریم.
برای راهحل کامل به صفحهی ۱۸۸ کتاب تحقیقی در آثار ریاضی ابوریحان بیرونی مراجعه کنید.
تصویر قضیهی ۱ و ۲ از کتاب: