حفر لوله
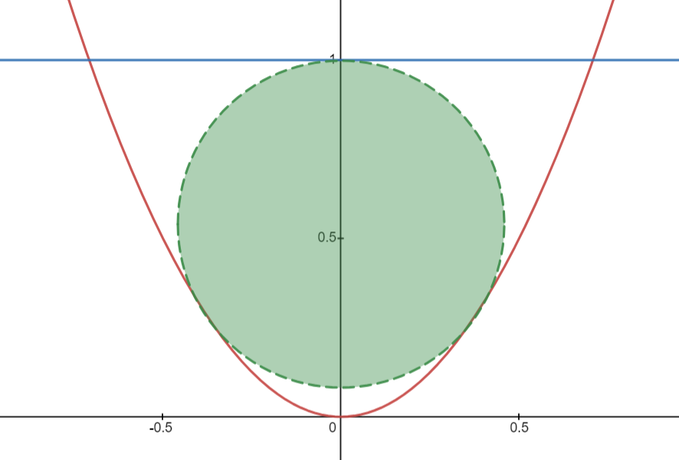
فرض کنیم یه کانال حفر شده داریم که سطح مقطعش با رابطه y=2x^2 تعریف میشه و عمقش یک متره، میخوایم تو این کانال بزرگ ترین لوله ممکن رو قرار بدیم. مختصات مرکز این لوله و شعاعش چقدره؟
(سوال پیشنهادی از @sali_va)
لینک مساله در توویتر: https://twitter.com/Riazi_Cafe/status/1705827665717137521
راهحل 1
شعاع دایره تقریبا برابر است با 0.4571.
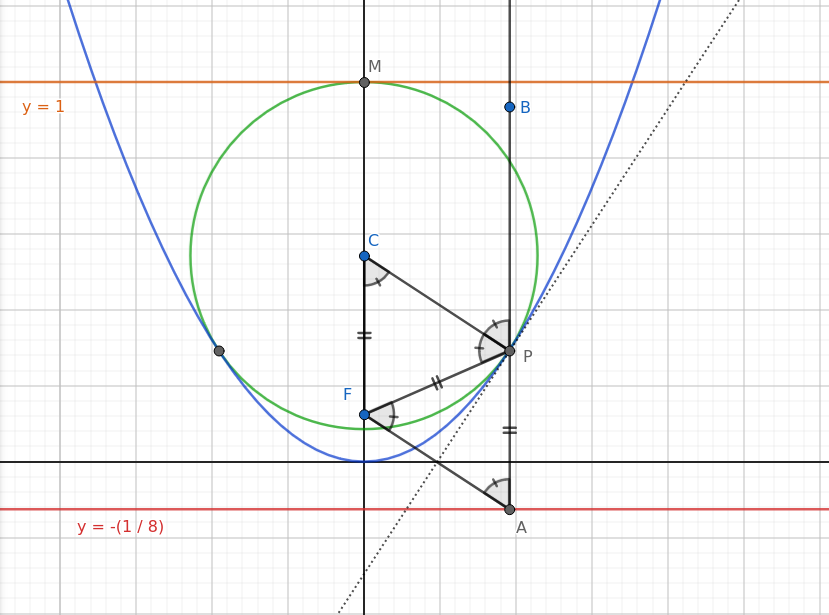
طبق تعریف، سهمی y=2x^2 مکان هندسی نقاطی هست که از کانون (Focus) به مختصات F: (x=0,y=1/8) و خط هادی (Directrix) با رابطه y=-1/8 فاصله یکسان داشته باشد.
بنابرین در نمودار زیر FP=AP و زوایای مجاور آنها در مثلث تشکیل شده هم برابرند.
همچنین طبق خاصیت بازتابی سهمی، پارهخطهای BP و FP با پارهخط عمود بر سهمی در نقطه P زاویه برابر می سازند، و طبق خاصیت دایره، پارهخط عمود در نقطهی P شعاع دایره است.
پس زوایای مشخص شده در شکل برابرند، و CFAP متوازیالاضلاع است و CF=AP. که از آن میتوان نتیجه گرفت C_y=P_y+1/4.
$$ \begin{aligned} CF = AP \implies& \\ C_y - F_y = P_y - A_y \implies& \\ C_y - \frac{1}{8} = P_y + \frac{1}{8} \implies& C_y=P_y+\frac{1}{4} \end{aligned} $$
از طرفی دیگر، اندازه شعاع دایره برابر است با R=1-C_y. پس CP=1-C_y. که اگر این را با در کنار C_y=P_y+1/4 قرار دهیم، C_y و R به دست میآید.
$$ \begin{aligned} CM = CP \implies& (1 - C_y)^2 = (C_y - P_y)^2 + (0 - P_x)^2 \\ \implies& (1 - C_y)^2 = \frac{1}{4}^2 + \frac{P_y}{2} \\ \implies& 1 - 2C_y + C_y^2 = \frac{1}{4}^2 + \frac{C_y-1/4}{2} \\ \implies& C_y^2 - \frac{5}{2}C_y + \frac{17}{16} = 0 \\ \implies& C_y = \frac{5}{4} - \frac{1}{\sqrt{2}}, R = \frac{1}{\sqrt{2}} - \frac{1}{4} \end{aligned} $$
راهحل 2
میتوان شیب پارهخط PC را به دو طریق مختلف نوشت: ۱. اینکه عمود بر مماس بر منحنی در نقطه P است، و ۲. از طریق اختلاف مختصات دو نقطهی P و C. که باز به رابطهی اول در راهحل قبلی میرسیم. بقیه راهحل مثل راهحل قبلی است.
$$ -\frac{1}{4 P_x} = \frac{P_y-C_y}{P_x-0} \implies P_y - C_y = -\frac{1}{4} $$