اژدها در صفحه شطرنج
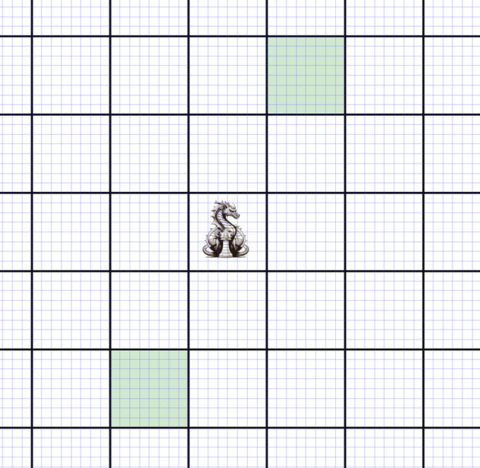
مهره اژدها مهرهایه که خونه ۲ تا بالا یکی راست و خونه ۲ تا پایین یکی چپ رو تهدید میکنه.
به چند حالت میشه ۳ تا مهرهی اژدها در صفحهی شطرنج ۸x۸ گذاشت به طوری که هیچ دوتایی همدیگه رو تهدید نکنند؟
لینک مساله در توویتر: https://twitter.com/Riazi_Cafe/status/1706574099131302222
پاسخ سوال برابر است با 39084
برای محاسبه آن، جدول ۸ در ۸ را تقسیم میکنیم به ۲۲ زنجیره به صورت زیر (رنگ خانه های هر زنجیره با هم یکی است)

دو اژدها در صورتی همدیگر را تهدید میکنند که در یک زنجیره و پس از یکدیگر قرار گرفته باشند. تعداد زنجیره های به طول ۴ برابر است با ۱۰ و تعداد هر یک از زنجیره های به طول ۳ و ۲ و ۱ برابر است با ۴.
در ادامه سعی میکنید حالاتی که حداقل دو اژدها همدیگر را تهدید میکندد را بشماریم. این حالات را میتوان به ۳ دسته تقسیم کرد:
- هر سه اژدها در یک زنجیره قرار دارند و دو جفت از آنها همدیگر را تهدید میکنند
- هر سه اژدها در یک زنجیره قرار دارند ولی فقط یک جفت از آنها همدیگر را تهدید میکنند
- یک جفت اژدها همدیگر را تهدید میکنند و اژدهای سوم در زنجیره متفاوتی قرار دارد
تعداد حالات دسته ۱ برابر است با 10*2 + 4 = 24 (دو به ازای هر زنجیره به اندازه ۴ و ۱ به ازای هر زنجیره به طول ۳)
تعداد حالات دسته ۲ برابر است با 2*10 = 20 (دو به ازای هر زنجیره به طول ۴)
تعداد حالات دسته ۳ برابر است با 3 * 10 * 60 + 2 * 4 * 61 + 1 * 4 * 62 = 2536.
پس تعداد کل حالاتی که حداقل دو اژدها همدیگر را تهدید میکنند برابر است با 2536 + 20 + 24 = 2580.
تعداد کل حالاتی که میتوان سه اژدها را در جدول قرار داد برابر است با c(64,3) = 41664. پس پاسخ برابر است با 41664 منهای 2580 مساوی 39084.