هر ۲ حالت را می‌توان با ۵ برش به مربع‌ها تقسیم کرد.

یک راه برای بریدن حالت ۶ در ۱۳ با ۵ برش:

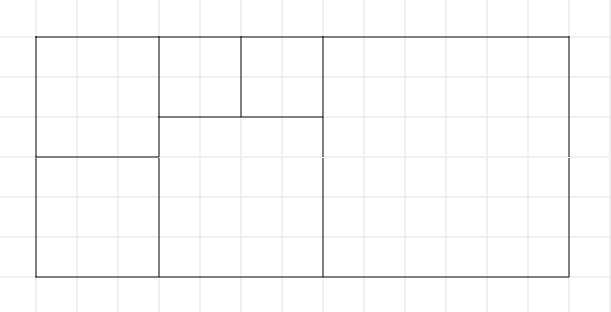
یک راه برای بریدن حالت ۹ در ۱۰ با ۵ برش:

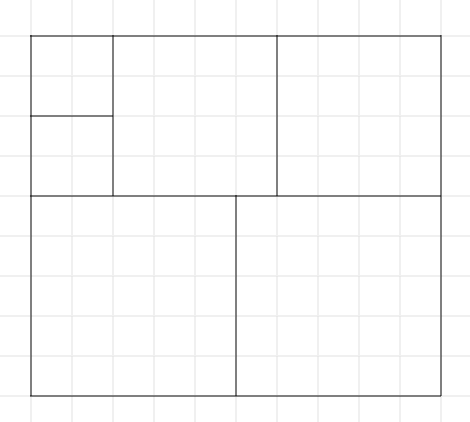
در ادامه توضیح می دهیم که چرا ۵ برش در هر دو مورد ضروری است.

تنها حالت‌هایی که صفر برش لازم دارد، حالت‌هایی است که طول و عرض (x, x) به ازای یک x طبیعی باشند. و حالت‌هایی که k بزرگتر از صفر برش نیاز دارند، حالت‌هایی هستند که پس از یک برش به ۲ مستطیل تقسیم شوند که یکی به i برش و دیگری به k-1-i برش نیاز داشته باشد.

پس اگر تمام نسبت‌های اضلاع را برای تعداد برش‌های کمتر از k داشته باشیم، می‌توانیم نسبت اضلاع‌هایی که k برش نیاز دارند را دربیاوریم.

به این ترتیب، برای تعداد برش‌های ۰ تا ۴ حالت‌های زیر بدست می‌آید:

• صفر برش: (x,x)
• ۱ برش: (x,2x)
• ۲ برش: (x,3x) و (2x,3x)
• ۳ برش: (x,4x) و (2x,5x) و (3x,4x) و (3x,5x)
• ۴ برش: (x,5x) و (2x,7x) و (3x,7x) و (3x,8x) و (4x,5x) و (4x,7x) و (5x,6x) و (5x,7x) و (5x,8x) و (6x,7x)

مثلا برای بدست آوردن لیست ۴ برش، چون پس از برش اول ۳ برش باقی می‌ماند، تک‌تک اعضای ۲ برش را به دو حالت عمودی و افقی در کنار تک‌تک اعضای ۱ برش قرار داده‌ایم، و همچنین تک‌تک اعضای ۳ برش را کنار تنها عضو صفر برش بصورت عمودی و افقی قرار داده‌ایم، و تکراری‌ها را به قرینه‌ی دوران ۹۰ درجه حذف کرده‌ایم.

مثلا اگر مستطیلی با نسبت‌های (1,2) را به صورت افقی کنار مستطیلی با نسبت‌های (2,3) قرار دهیم، مستطیلی با نسبت‌های (7,6) بدست می‌آید. و اگر آن‌ها را بصورت عمودی کنار هم قرار دهیم، مستطیلی با نسبت‌های (2,7) بدست می‌آید.

با توجه به اینکه هیچ‌کدام از 13x6 و 9x10 در بین نسبت‌های بالا نیست، پس با ۴ برش یا کمتر نمی‌شود این ۲ مستطیل را به تعدادی مربع تقسیم کرد و ۵ برش لازم است.