شکل زیر یک نمونه از سوراخ کردن مکعب را نشان می‌دهد (اشتراک قسمت شطرنجی و مکعب از داخل مکعب حذف شده).

سوراخ کردن مکعب باید به صورتی باشه که بتوان یک نخ از داخل آن عبور داد و با گره زدن دو سر نخ مکعب را آویزان کرد به طوری که نتوان بدون پاره کردن نخ مکعب را پایین کشید.

به طور مثال با چنین سوراخی نمی‌توان با گره زدن دو سر نخ مکعب را آویزان کرد.

عبور مکعب دوم از داخل معکب اول باید طوری باشد که مکعب دوم بتواند یک دور کامل دور نخ فرضی که مکعب اول از آن آویزان است بزند

این مسئله به نام مسئله مکعب شاهزاده روپرت شناخته شده است طول ضلع بزرگترین مکعبی که می‌تواند از داخل مکعب اول عبور کند برابر است با

$$\frac{3\sqrt{2}}{4} \approx 1.0606601$$

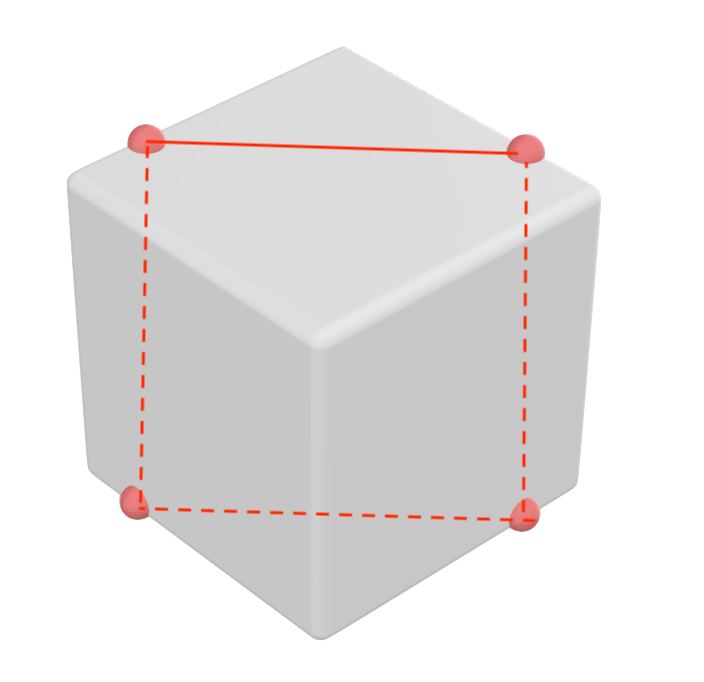
دو نقطه را روی دو ضلع مجاور مکعب قرار دهید به طوری که فاصله هرکدام از نقطه تلاق دو ضلع 3/4 باشد سپس دو نقطه دیگه را با قرینه کردن این دو نقطه (مطابق شکل) بر روی مکعب قرار دهید این چهار نقطه مربعی با طول ضلع $\frac{3\sqrt{2}}{4} \approx 1.0606601$ تشکیل می‌دهند.

حالا این مربع را به صورت عمود بر خودش در فضای سه بعدی گسترش دهید تا یک شکل سه بعدی تولید کند. مربع دوم می‌تواند در جهت گسترش این شکل از داخل مربع اول عبور کند.