شمارش گرافهای ناهمگون
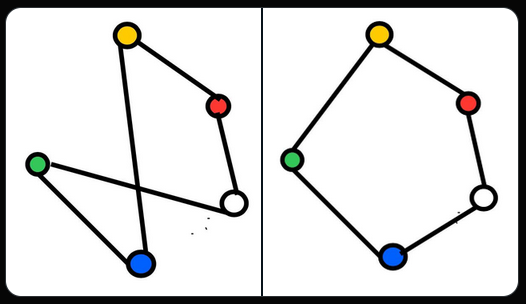
تعداد گراف های ۵ راسی بدون وزن بدون جهت با راس های شماره ۱ تا ۵ برابر است با ۱۰۲۴. دو گراف همگون هستند اگر بتوان با تغییر شماره راس ها آنها را بهم هم تبدیل کرد. مثل ۲ گراف در تصویر.
بدون استفاده از کامپیوتر به دست بیارید چند گراف ناهمگون ۵ راسی وجود داره؟
لینک سوال در توویتر: https://twitter.com/Riazi_Cafe/status/1733020112616292419
راه حل برابر با \(34\) است.
از این به بعد، وقتی از اصطلاح گراف با \(n\) رأس استفاده میکنیم، منظور ما گراف بدون وزن و بدون جهت است که رأسهای آن با اعداد \(1, 2, 3, \ldots, n\) برچسبگذاری شدهاند. فرض کنید \(G\) یک گراف با \(n\) رأس و \(P = \langle p_1, p_2, \ldots, p_n \rangle\) یک جایگشت از اعداد \(1\) تا \(n\) باشد. ما تبدیل گراف \(G\) توسط جایگشت \(P\) را به عنوان گرافی مشابه \(G\) تعریف میکنیم با این تفاوت که برچسب هر رأس \(i\) با \(p_i\) جایگزین میشود. این تبدیل را با \(T(G, P)\) نشان میدهیم. ما از قضیه زیر برای شمارش تعداد گرافهای ناهمگون با 5 رأس استفاده میکنیم. اثبات این قضیه را به انتهای راه حل موکول میکنیم. لم 1. برای یک \(n\) داده شده، فرض کنید \(x_n\) تعداد جفتهای \((G, P)\) باشد به طوری که \(G\) یک گراف با \(n\) رأس، \(P\) یک جایگشت از اعداد \(1,2, \ldots, n\)، و \(T(G, P) = G\) باشد. تعداد گرافهای ناهمگون با \(n\) رأس برابر با \(x_n/n!\) است.
بر اساس قضیه، پاسخ این سوال برابر با \(x_5 / 120\) است. بنابراین، هدف ما یافتن مقدار \(x_5\) است.
ما میتوانیم جایگشتهای اعداد \(1, 2, \ldots, n\) را بر اساس طول دورههای گراف جایگشت آنها دستهبندی کنیم:
5 دور اندازه 1: \(\langle 1, 2, 3, 4 ,5 \rangle\) تنها جایگشتی است که گراف جایگشت آن 5 دور دارد. همه \(2^{10}\) گراف با 5 رأس تحت این جایگشت دست نخورده باقی میمانند.
3 دور اندازه 1 و 1 دور اندازه 2: 10 جایگشت وجود دارد که گراف جایگشت آنها 3 دور اندازه 1 و 1 دور اندازه 2 دارد. \(2^{7}\) گراف با 5 رأس تحت چنین جایگشتهایی دست نخورده باقی میمانند.
2 دور اندازه 1 و 1 دور اندازه 3: 20 جایگشت وجود دارد که گراف جایگشت آنها 2 دور اندازه 1 و یک دور اندازه 3 دارد. \(2^{4}\) گراف با 5 رأس تحت چنین جایگشتهایی دست نخورده باقی میمانند.
1 دور اندازه 1 و 1 دور اندازه 4: 30 جایگشت وجود دارد که گراف جایگشت آنها 1 دور اندازه 1 و 1 دور اندازه 4 دارد. \(2^{3}\) گراف با 5 رأس تحت چنین جایگشتهایی دست نخورده باقی میمانند.
1 دور اندازه 2 و 1 دور اندازه 3: 20 جایگشت وجود دارد که گراف جایگشت آنها 1 دور اندازه 2 و 1 دور اندازه 3 دارد. \(2^{3}\) گراف با 5 رأس تحت چنین جایگشتهایی دست نخورده باقی میمانند.
1 دور اندازه 1 و 2 دور اندازه 2: 15 جایگشت وجود دارد که گراف جایگشت آنها 1 دور اندازه 1 و دو دور اندازه 2 دارد. \(2^{6}\) گراف با 5 رأس تحت چنین جایگشتهایی دست نخورده باقی میمانند.
1 دور اندازه 5: 24 جایگشت وجود دارد که گراف جایگشت آنها 1 دور اندازه 5 دارد. 4 گراف با 5 رأس تحت چنین جایگشتهایی دست نخورده باقی میمانند.
بنابراین، \(x_5 = 2^{10} + 10\cdot 2^7 + 20\cdot 2^4 + 30\cdot 2^3 + 20\cdot 2^3 + 15\cdot 2^6 + 4!\cdot 4 = 4080\). بنابراین، پاسخ برابر با \(4080/120 = 34\) است.
اثبات. اثبات قضیه. یک ابرگراف با \(2^{\binom{n}{2}}\) رأس در نظر بگیرید که هر راس متناظر با یک گراف \(n\) رأسی است. برای هر جایگشت \(P\)، یک یال بین رأس \(u\) و رأس \(v\) با برچسب \(P\) رسم میکنیم اگر \(T(u) = v\) باشد. تعداد گرافهای ناهمگون با \(n\) رأس برابر است با تعداد مؤلفههای متصل این ابرگراف. توجه داشته باشید که درجات تمامی رئوس این ابرگراف برابر با \(n!\) است. علاوه بر این، تمام رئوس هر مؤلفه متصل نماینده گرافهای همگون هستند. این بدان معناست که برای هر مؤلفه متصل، تعداد یالها بین هر جفت رأس یکسان است، و این مقدار برابر است با تعداد حلقههای هر رأس درون آن مؤلفه. بنابراین، جمع تعداد حلقههای رئوس در هر مؤلفه برابر است با \(n!\). این بدان معناست که کل تعداد حلقهها بر روی \(n!\) برابر است با تعداد مؤلفههای ابرگراف که برابر است با تعداد گرافهای ناهمگون با اندازه \(n\).