پاسخ برابر با ۱٫۵ سانتی‌متر مربع است.

منبع ما برای این سوال این ویدئو از کانال 3Blue1Brown بود: https://youtu.be/ltLUadnCyi0

ابتدا بیان می‌کنیم که هر خط عمودی که تصویر آن روی زمین در سایه مکعب قرار دارد، دقیقاً در دو نقطه مکعب را قطع می‌کند (به جز موارد لبه که در بحث ما مهم نیستند). این بدان معناست که مساحت کل سایه مکعب برابر با نصف مجموع مساحت‌های سایه‌های اضلاع آن است. از آنجایی که مکعب دارای 6 ضلع با مساحت‌های مساوی است، میانگین مساحت سایه مکعب برابر با سه برابر میانگین مساحت یک ضلع از مکعب است.

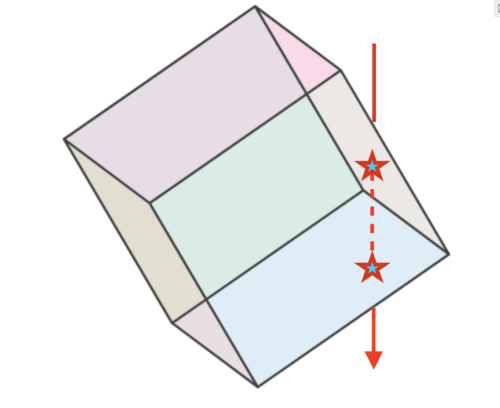
حال، یک وجه از مکعب را که مربعی به ابعاد 1 در 1 سانتی‌متر است در نظر بگیرید. مساحت سایه یک مربع چرخیده شده برابر است با مساحت مربع ضربدر (قدر مطلق) کسینوس زاویه بین بردار نرمال آن وجه و محور z.

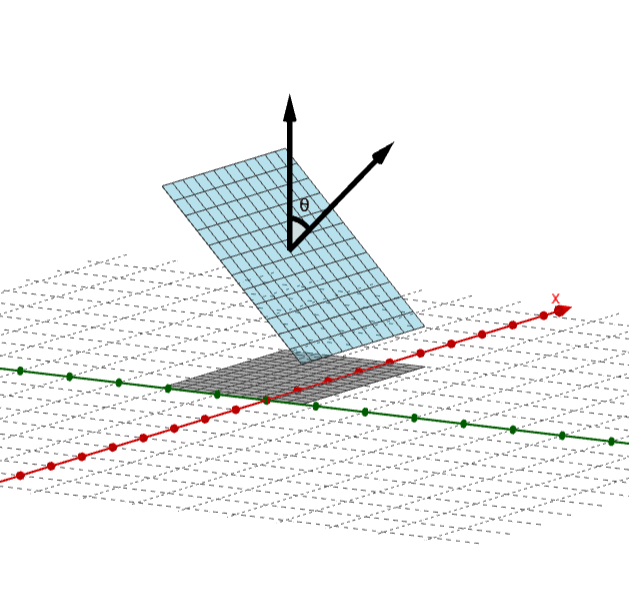
هر چند بردار نرمال تصادفی است و زاویه بین این بردار و محور z‎ در بازه‌ی ‏$‎(0,\pi)‏$‎ قرار دارد، اما این زاویه به صورت یکنواخت از ‏$‎(0,\pi)‏$ انتخاب نمی‌شود.

همه‌ی بردارهای نرمال کره‌ای به شعاع ۱ را تشکیل می‌دهند. چون توزیع جهت چرخش را یکنواخت فرض کردیم، پس احتمال اینکه برداری عضو زیرمجموعه A از کل بردارها باشد، متناسب است با مساحتی که آن زیرمجموعه روی کره مشخص می‌کند. بنابراین، احتمال اینکه زاویه یک بردار تصادفی با محور z‎ در بازه‌ی $(\theta, \theta+\Delta\theta‏)‏$‎ باشد، برابر است با مساحت حلقه‌ای روی کره که این بازه آن را مشخص می‌کند تقسیم بر مساحت کل کره.

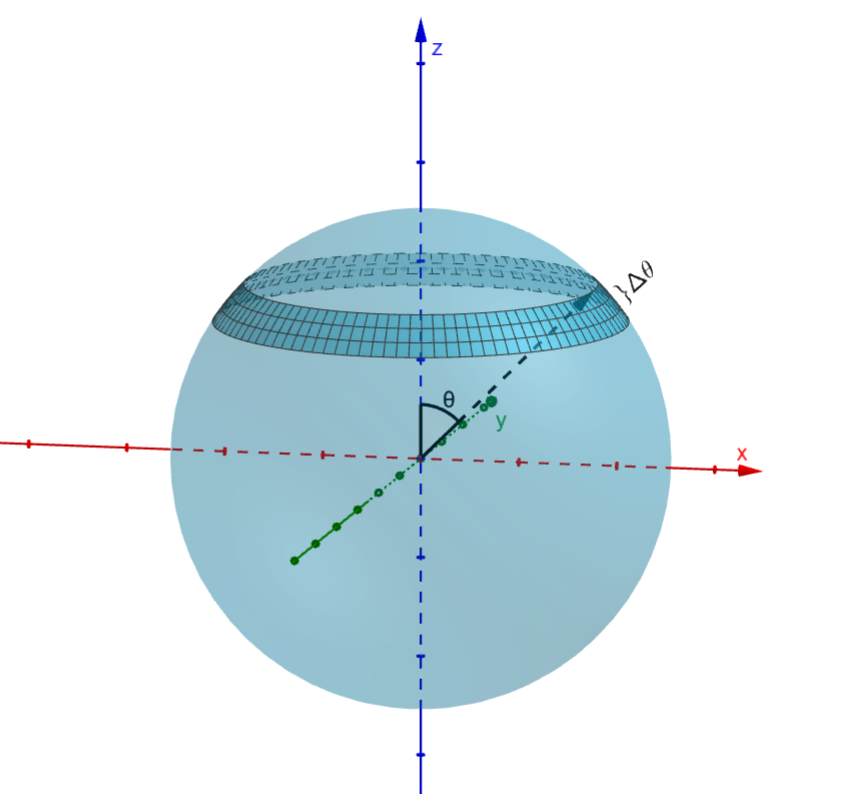
وقتی ‏$‎\Delta\theta‏$‎ بسیار کوچک است، این حلقه را می‌توان استوانه‌ای در نظر گرفت که شعاع آن ‏$‎sin(\theta)$ و ارتفاع آن ‏$‎\Delta\theta‏$‎ است. پس مساحت این حلقه برابر خواهد شد با ‏$‎2\pi \cdot sin(\theta) \cdot \Delta\theta$. بنابراین با توجه به اینکه مساحت کره با شعاع ۱ برابر است با ‏$‎4\pi$، احتمال اینکه زاویه بردار در بازه $(\theta, \theta+\Delta\theta‏)‏$‎ باشد برابر خواهد بود با $\frac{‎2\pi \cdot sin(\theta) \cdot \Delta\theta}{4\pi}$.

پس تابع چگالی احتمال (pdf) توزیع بردارها $‎\frac{2\pi \cdot sin(\theta)}{4\pi} = sin(\theta)/2$ است و امیدریاضی تابع $f(\theta)‏$‎ برابر با ‏$‎\int_{0}^{\pi} f(\theta) \frac{sin(\theta)}{2} \cdot d\theta$ است.

بنابراین، اگر $f(\theta)‏$ را برابر با مساحت وجهی از مکعب که بردار نرمال آن با محور z زاویه $\theta$ را می‌سازد قرار دهیم، میانگین مساحت سایه مربع برابر است با $‎\int_{0}^{\pi} |cos(\theta)| \cdot ‎\frac{sin(\theta)}{2} \cdot d\theta = \int_{0}^{\pi/2}sin(\theta) \cdot cos(\theta) \cdot d\theta =1/2$.

و چون میانگین مساحت سایه مکعب برابر با ۳ برابر میانگین سایه یکه وجه بود، پاسخ مورد نظر برابر با ‏$‎3/2 cm^2‏$‎ است.