در بهترین راه حل، ما آنتن‌ها را در مکان‌های $(1/16,0.5), (9/16,0.25),(9/16,0.75)$ قرار می‌دهیم و دورترین نقاط از این آنتن‌ها، نقاط قرمز رنگ در شکل زیر خواهند بود که فاصله آنها تا نزدیکترین آنتن $\frac{\sqrt{1/8^2 + 1}}{2} \simeq 0.503891$ خواهد بود.

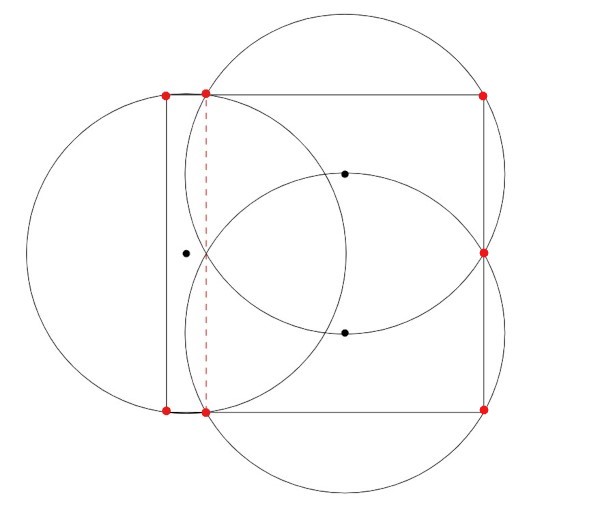
ما به این مسئله به شکل زیر فکر می‌کنیم: کوچکترین شعاع $r$ و سه نقطه $a$, $b$, $c$ را پیدا کنیم، به طوری که سه دایره با شعاع $r$ متمرکز بر $a,b, c$ یک مربع با اضلاعی به طول واحد را پوشش دهند. از آنجا که ما فقط سه دایره داریم، یک ضلع از مربع باید به طور کامل توسط یکی از دایره‌ها پوشیده شود. فرض کنید که این لبه از مربع، لبه عمودی سمت چپ باشد و $a$ مرکز دایره‌ای باشد که آن را می‌پوشاند. به دلیل تقارن، می‌دانیم که یک راه حل بهینه وجود دارد که در آن مختصات $y$ از $a$ برابر 0.5 است. فرض کنید $x$ مختصات $x$ از $a$ باشد. بنابراین، $ r \geq \sqrt{x^2 + 0.5^2}$ به طوری که $a$ دو نقطه انتهایی آن ضلع از مربع را پوشش دهد. از طرفی دیگر، از آنجا که دو دایره باقیمانده باید یک مستطیل به اندازه $(1-2x) \times 1$ را پوشش دهند، ما همچنین داریم $r \geq \sqrt{((1-2x)/2) ^ 2 + 0.25 ^ 2}$. بنابراین، باید یک $r$ را پیدا کنیم که عبارت زیر را حداقل کند:

$$\max_{0 \leq x \leq 1}{\sqrt{((1-2x)/2) ^ 2 + 0.25 ^ 2}, \sqrt{x^2 + 0.5^2}}$$

این عبارت زمانی به حداقل می‌رسد که $\sqrt{((1-2x)/2) ^ 2 + 0.25 ^ 2} = \sqrt{x^2 + 0.5^2}$ که به این معنی است $((1-2x)/2) ^ 2 + 0.25 ^ 2 = x^2 + 0.5^2$ و بنابراین $x = 1/16$. مقدار حداقل $r$ خواهد بود ‏$\frac{\sqrt{1/8^2 + 1}}{2} \simeq 0.503891$.