راه‌حل ۱

پاسخ «نه» است.

وضعیت نهایی هر خانه جدول، تابعی است از اینکه تعداد عمل‌های 2x2 یا 3x3 که شامل آن خانه است زوج است یا فرد. بنابراین، (۱) ترتیب عمل‌ها مهم نیست، (۲) می‌توانیم فرض کنیم هر زیرجدول 2x2 یا 3x3 صفر یا یک بار انتخاب شده است، زیر اثر دوبار انتخاب کردن یک زیرجدول برابر است با صفر بار انتخاب کردن آن.

پس مساله را می‌توان به صورت یک تابع F مدل کرد که ورودی آن زیرمجموعه‌ای از تمام زیرجدول‌های 2x2 یا 3x3 ممکن است، و خروجی آن حالت نهایی جدول صفر و یک. و سوالی که می‌خواهیم پاسخ دهیم این است که آیا این تابع پوشا است یا نه؟ یعنی آیا می‌تواند تمام حالت‌های نهایی جدول صفر و یک را تولید کند یا نه.

اگر دقت کنیم، با توجه به اینکه ۱۶ زیرجدول 2x2 و ۹ زیرجدول 3x3 داریم و برای انتخاب هر زیرجدول ۲ حالت داریم، اندازه دامنه این تابع $2^{9+16}=2^{25}$ است. اندازه برد این تابع هم با توجه به اینکه جدولمان ۲۵ خانه دارد و هر خانه ۲ حالت می‌تواند بگیرد، $2^{25}$ است.

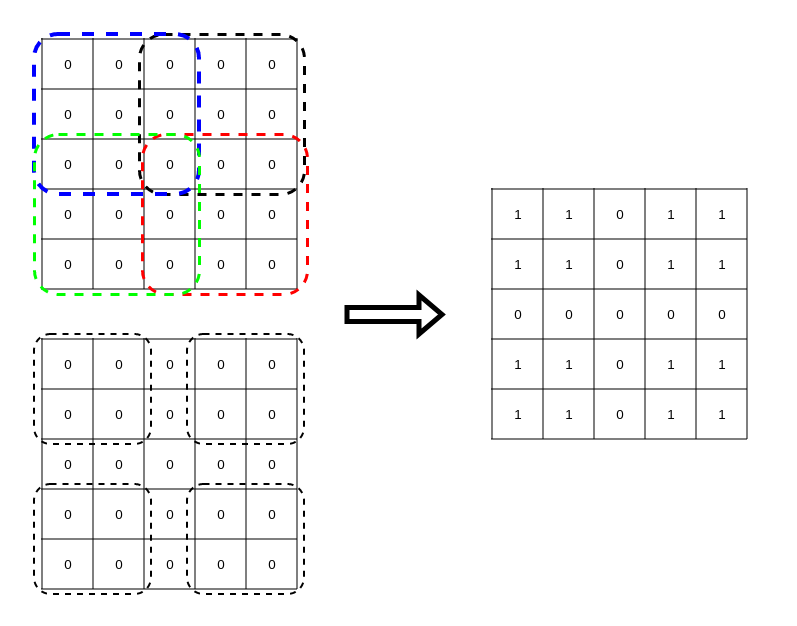
اگر ۲ عضو از دامنه پیدا کنیم که مقدار خروجی تابع به ازای آن دو یکسان باشد، با توجه به برابر بودن اندازه دامنه و برد تابع، نتیجه خواهیم گرفت که تابع پوشا نیست. اگر دقت کنیم، اگر ۴ زیرجدول 3x3 گوشه‌ای را انتخاب کنیم یا اگر ۴ زیرجدول 2x2 گوشه‌ای را انتخاب کنیم، هر دو نتیجه نهایی یکسان می‌دهد. پس تابع پوشا نیست و پاسخ مساله‌ی اصلی نه است.

راه‌حل ۲

راه‌حل از: Amirhosein

فرض کنید ردیف اول و چهارم جدول را مانند شکل زیر خاکستری رنگ کنیم:

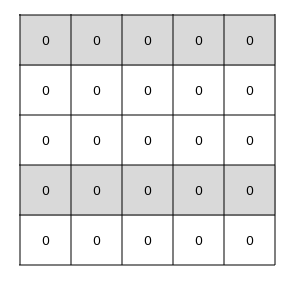
در این صورت هر زیرجدول 2x2 یا 3x3 ای که انتخاب کنیم، با بخش سفید به تعداد زوج خانه اشتراک خواهد داشت. بنابراین هر حرکت تعداد زوجی خانه سفید را برعکس خواهد کرد و زوجیت مجموع خانه‌های سفید ثابت خواهد ماند. با توجه به اینکه در ابتدا مجموع خانه‌های سفید صفر است، پس به حالت‌هایی که مجموع خانه‌های سفید فرد است نمی‌توانیم برسیم و پاسخ مساله اصلی نه است.