کاشیکاری جدول ۱۰x۱۰

روی جدولی ۱۰x۱۰ میخواهیم تعدادی کاشی ۱x۵ و ۵x۱ قرار دهیم به طوری سطح هیچ دو کاشیای همپوشانی نداشته باشد.
کمترین تعداد کاشی که میتوان گذاشت بطوری که جا برای یک کاشی دیگر نباشد چند است؟
توضیحات.
- دو کاشی میتوانند هممرز باشند، ولی سطح آنها نباید اشتراک داشته باشد.
- کاشیها نمیتوانند از وسط یک خانه جدول شروع شوند و هر کاشی باید ۵ خانه جدول را به طور کامل بپوشاند.
منبع سوال: Crux Mathematicorum, Vol. 6, No. 2, February 1980.
لینک سوال در توویتر: https://twitter.com/Riazi_Cafe/status/1759114261920727511
پاسخ مساله برابر با ۱۱ است. یک نمونه کاشیکاری با ۱۱ کاشی در شکل زیر آمده است.
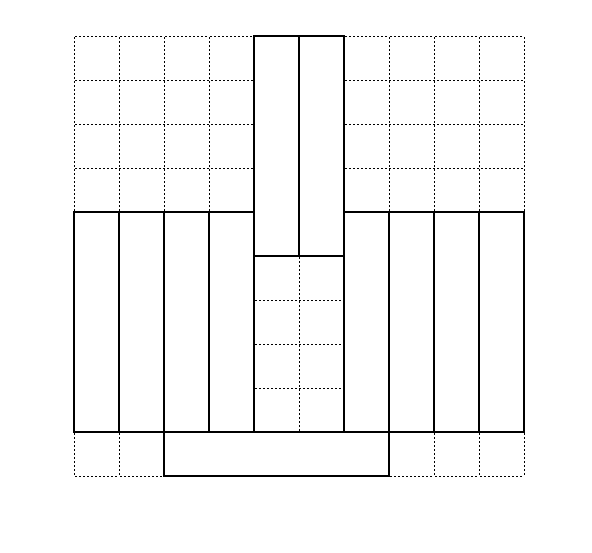
و به طور کلی برای کاشیکاری جدول $2n\times2n$ با کاشیهای به طول n، پاسخ برابر است با $2n+1$ که با تعمیم دادن کاشیکاری بالا به n دلخواه بدست میآید.
در ادامه به این میپردازیم که چرا با $2n$ کاشی نمیشود.
لم ۱. اگر با $2n$ کاشی بتوان کاشیکاری کرد، آنگاه حداقل یک کاشی افقی و حداقل یک کاشی عمودی وجود دارد.
اثبات. با استفاده از برهان خلف اثبات میکنیم. فرض کنید همه $2n$ کاشی عمودی باشند. آنگاه هر ستون باید شامل حداقل یک کاشی باشد، وگرنه میتوان یک کاشی دیگر در آن ستون اضافه کرد. از طرفی دیگر، کاشی موجود در هیچکدام از ستونها نمیتواند از سطر ۱ شروع شود، زیر در آنصورت در پایین آن کاشی در همان ستون میتوان یک کاشی دیگر اضافه کرد. بنابراین سطر اول خالی است. بنابراین یک کاشی افقی دیگر میتوان در سطر اول اضافه کرد و کاشیکاری با $2n$ کاشی عمودی با شرایط مساله در تناقض است. پس فرضمان اشتباه بود و همه $2n$ کاشی نمیتوانند عمودی باشند.
به طور مشابه میتوان اثبات کرد که همه $2n$ کاشی نمیتوانند افقی باشند.
پس حداقل یک کاشی عمودی و حداقل یک کاشی افقی وجود دارد.
لم ۲. اگر ستون $k <= n$ شامل یک کاشی عمودی باشد، آنگاه همهی ستونهای ۱ تا $k-1$ نیز شامل کاشیهای عمودی هستند.
اثبات. مستطیل بین کاشی عمودی و لبه چپ جدول را در نظر بگیرید (مثل مستطیل سبز رنگ در شکل زیر). چون عرض این مستطیل کمتر از n است، نمیتواند شامل هیچ کاشی افقی باشد. بنابراین اگر یکی از ستونهای ۱ تا $k-1$ خالی باشد، آنگاه حتما یکی از ستونهای بخش سبز رنگ نیز خالی است، که با شرط مساله (جا برای کاشی دیگری نباشد) در تناقض است.
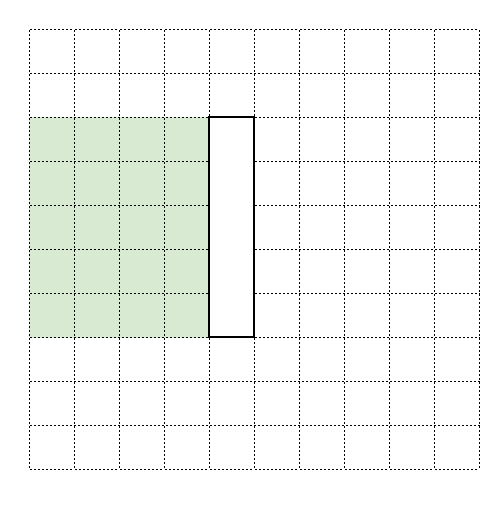
نتایج از لم ۲.
- به طور مشابه، اگر ستون $k > n$ شامل یک کاشی عمودی باشد، آنگاه همه ستونهای $k+1$ تا $2n$ نیز شامل کاشیهای عمودی هستند.
- به طور مشابه، لم ۲ و نتیجه ۱ برای سطرها نیز برقرار است.
لم ۳. با $2n$ کاشی نمیتوان شرایط مساله را برآورده کرد.
اثبات. فرض کنیم یک کاشیکاری با کمتر یا مساوی $2n$ کاشی داریم که جا برای یک کاشی دیگر نباشد. در اینصورت حداقل تعداد یکی از کاشیهای افقی یا عمودی کمتر یا مساوی $n$ است. فرض کنید کاشیهای عمودی کمتر یا مساوی $n$ باشند.
- در اینصورت، طبق لم ۲ همه این کاشیهای عمودی در تعدادی ستون پشتسرهم ابتدایی و تعدادی ستون پشتسرهم انتهایی قرار دارند و حداقل $n$ ستون پشتسرهم در میانه توسط هیچ کاشی عمودی بلاک نشده است.
- طبق لم ۱ هم تعداد کاشیهای عمودی حداقل ۱ است، و با توجه به اینکه فرض کردیم تعداد کل کاشیها حداکثر $2n$ است، پس تعداد کاشیهای افقی کمتر یا مساوی $2n-1$ میشود. مانند نکته بالا، این یعنی اینکه حداقل یک سطر هم در میانه جدول توسط هیچ کاشی افقی بلاک نشده است.
طبق نکات بالا نتیجه میگیریم که در این چینش باید جا برای یک کاشی افقی دیگر باشد، پس فرض اولیه اشتباه بود و با حداکثر $2n$ کاشی نمیتوان شرایط مساله را برآورده کرد.