آپدیت: راه‌حلی که در ادامه آمده درست نیست و قراره به روز رسانی بشه

پاسخ π + 1 است.

ابتدا ثابت می‌کنیم که اگر سرعت گربه کمتر از π + 1 برابر سرعت موش باشد، راهی برای موش وجود دارد که از دایره فرار کند. به خاطر داشته باشید که شعاع دایره اصلی 1 متر است. حالا، دایره قرمز تخیلی را در نظر بگیرید که مرکز آن همان مرکز دایره مسئله است اما شعاع آن $1/(1+\pi)$ متر است.

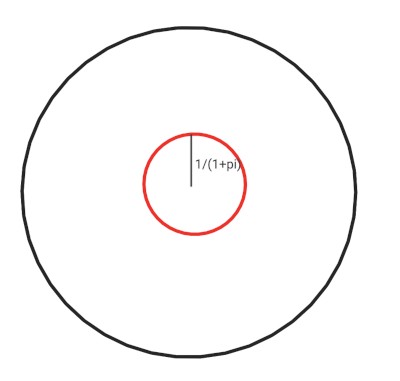در این حالت، موش می‌تواند با استراتژی زیر از دایره سیاه فرار کند:

1. موش ابتدا به سمت یک نقطه دلخواه از دایره قرمز حرکت می‌کند بدون اینکه به حرکت گربه اهمیت دهد.
2. زمانی که موش به نقطه‌ای از دایره قرمز می‌رسد، فقط بر روی محیط دایره قرمز حرکت می‌کند. «تصویر مکان گربه» بر روی دایره قرمز را تقاطع محیط دایره قرمز با پاره‌خط واصل مکان گربه و مرکز دایره‌ها تعریف کنیم. اگر این پاره‌خط را از طرف دیگر گسترش دهیم، در یک نقطه دیگر که مقابل تقاطع اول است، دایره قرمز را قطع می‌کند. ما این نقطه دوم را «تصویر مقابل مکان گربه» بر روی دایره قرمز می‌نامیم.

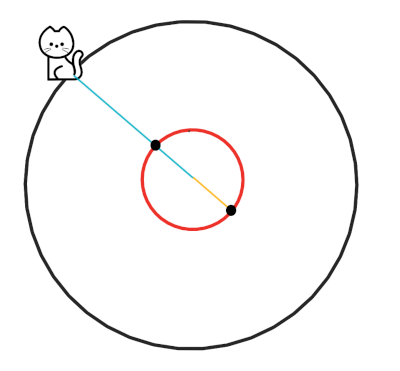
در این مرحله، موش همیشه به سمت تصویر مقابل مکان گربه بر روی دایره قرمز حرکت می‌کند. با توجه به اینکه گربه بر روی دایره‌ای با شعاع π + 1 برابر شعاع دایره قرمز حرکت می‌کند اما سرعت آن کمتر از π + 1 برابر سرعت موش است، موش نهایتاً می‌تواند به تصویر مقابل مکان گربه بر روی دایره قرمز برسد.

3. به محض رسیدن موش به تصویر مقابل مکان گربه بر روی دایره قرمز، مستقیماً به سمت نزدیک‌ترین نقطه دایره سیاه می‌رود. با توجه به اینکه شعاع دایره قرمز $1/(1+\pi)$ و شعاع دایره سیاه 1 است، پس فاصله‌ای که موش باید طی کند $1-1/(1+\pi) = \pi / (\pi+1)$ است. برای اینکه گربه بتواند موش را بگیرد، باید مسافتی برابر با $\pi$ طی کند. با این حال، از آنجا که سرعت گربه کمتر از $1+\pi$ برابر سرعت موش است، موش می‌تواند زودتر از گربه به آن نقطه برسد و بنابراین از دایره فرار کند.

حال نشان می‌دهیم که اگر سرعت گربه حداقل $1+\pi$ برابر سرعت موش باشد، همیشه می‌تواند موش را بگیرد. استراتژی گربه در این حالت آسان است. تا زمانی که موش در داخل دایره قرمز حرکت می‌کند، گربه اصلاً حرکت نمی‌کند. به محض اینکه موش از دایره قرمز خارج شود، گربه همیشه به سمت نقطه‌ای در دایره سیاه حرکت می‌کند که به موش نزدیک‌تر است. از آنجا که سرعت گربه حداقل $1+\pi$ برابر سرعت موش است، و در هر زمان فاصله‌ای که گربه باید طی کند حداکثر $1+\pi$ برابر فاصله‌ای است که موش برای فرار از دایره باید طی کند، گربه همیشه می‌تواند موش را هنگامی که به محیط دایره سیاه رسید بگیرد.