پاسخ $11^9$ است. به طور کلی اگر $n$ راننده و $n$ جای پارکینگ داشته باشیم، پاسخ $(n+1)^{n-1}$ است.

راه‌حل اول

مساله را به این صورت تغییر می‌دهیم: مثل مساله‌ی اصلی ‏$‎n‏$‎ راننده داریم ولی یک جای پارکینگ دیگر اضافه می‌کنیم، و این ‏$‎n+1‏$‎ جای پارکینگ را دایره‌وار و در جهت ساعتگرد کنار هم قرار می‌دهیم. هر کس یک جای پارکینگ مورد علاقه دارد و راننده‌ها به ترتیب وارد می‌شوند و هر کس از جای پارکینگ مورد علاقه خود شروع می‌کند و در دایره در جهت ساعتگرد حرکت می‌کند و در اولین جای پارکینگ خالی پارک می‌کند.

در این مساله‌ی تغییر یافته همه می‌توانند پارک کنند و در پایان یکی از خانه‌ها خالی می‌ماند. یک حالت تخصیص جاهای مورد علاقه در مساله‌ی تغییر یافته جزو حالت‌های مطلوب در مساله‌ی اصلی است اگر و تنها اگر در مساله‌ی تغییر یافته خانه‌ی خالی مانده خانه‌ی $n+1‏$‎ ام باشد.

در مساله‌ی تغییر یافته چون هر کس ‏$‎n+1‏$‎ گزینه برای جای پارکینگ مورد علاقه‌اش دارد، $(n+1)^n$ حالت تخصیص جاهای مورد علاقه وجود دارد. همچنین در مساله‌ی تغییر یافته اگر حالت تخصیص جاهای مورد علاقه ‏$‎(a_1,...,a_n)$ منجر به خالی ماندن خانه‌ی $x$ شود، در اینصورت حالت تخصیص ‏$‎(a_1+d,...,a_n+d)\mod(n+1)‏$‎ منجر به خالی ماندن خانه‌ی ‏$‎(x+d)\mod(n+1)‏$‎ خواهد شد. پس به ازای یک حالت تخصیص خاص، دقیقا یکی از مقادیر $d=0..n‏$‎ منجر به خالی ماندن خانه‌ی ‏$‎n+1‏$‎ ام میشود و جزو حالت‌های مطلوب مساله‌ی اصلی نیز هست.

بنابراین تعداد کل حالت‌های مطلوب مساله‌ی اصلی ‏$\frac{(n+1)^n}{n+1}‏=(n+1)^{n-1}‏$‎‎ است.

این استدلال منسوب به Henry O. Pollak است و در منابع مختلف مثل صفحه ویکی‌پدیای مساله آمده.

راه‌حل دوم

تعداد حالت‌های تخصیص جای مورد علاقه‌ی مطلوب برای $n‏$‎ راننده و ‏$‎n‏$‎ جای پارکینگ متوالی را ‏با ‏$‎F(n)‏$‎ نشان می‌دهیم.

فرض کنید نفر آخر در خانه‌ی $i$ پارک کند. در اینصورت:

• ‏با توجه به اینکه موقع ورود نفر آخر خانه $i$ خالی است، پس $‎i-1‏$‎ نفر از نفرات قبلی جای مورد علاقه‌شان بین 1 تا $i-1‏$‎ است و $‎n-i‏$‎ نفر از نفرات قبلی جای مورد علاقه‌شان بین ‏$‎i+1‏$‎ تا ‏$‎n‏$‎ است.
• ‏جای مورد علاقه نفر آخر بین ‏1 تا ‏$‎i‏$‎ است.

بنابراین برای شمردن تعداد حالت‌های تخصیص مطلوبی که منجر به پارک کردن نفر آخر در جای ‏$‎i‏$‎ می‌شود باید:

• ‏$‎i-1‏$‎ نفر از ‏$‎n-1‏$‎ نفر قبلی را انتخاب کنیم که در ‏$‎i-1‏$‎ جای اول پارک کنند (‏‏$‎{n-1}\choose{i-1}‏$‎‎ انتخاب).
• برای این ‏$‎i-1‏$‎ نفر حالت تخصیص جای مورد علاقه‌ای را انتخاب کنیم که همگی بتوانند در ‏$‎i-1‏$‎ خانه‌ی پشت سر هم پارک کنند (‏$‎F(i-1)‏$‎ انتخاب).
• برای ‏$‎n-i‏$‎ نفر دیگر حالت تخصیص جای مورد علاقه‌ای را انتخاب کنیم که همگی بتوانند در ‏$‎n-i‏$‎ خانه‌ی پشت سر هم پارک کنند ($F(n-i)‏$‎ انتخاب).
• و از بین ‏$‎i‏$‎ خانه‌ی اول یکی را به عنوان جای مورد علاقه‌ی نفر آخر انتخاب کنیم.

پس تعداد حالت‌های تخصیص مطلوبی که منجر به پارک کردن نفر آخر در جای ‏$‎i‏$‎ می‌شود برابر است با ‏‏$‎‏{n-1 \choose i-1} \cdot F(i-1) \cdot F(n-i) \cdot i$‎‎ و با جمع زدن حالت‌های مختلف جای پارک نفر آخر رابطه‌ی کلی مساله‌ی اصلی می‌شود:

$$ F(n) = \sum_{i=1}^n ‎{n-1 \choose i-1} \cdot F(i-1) \cdot F(n-i) \cdot i‏ $$

با قرار دادن حالت پایه‌ی $F(0)=1‏$‎ به آسانی می‌توان رابطه بازگشتی بالا را توسط برنامه‌سازی پویا در کامپیوتر پیاده‌سازی کرد و برای $F(10)‏$‎ مقدار $11^9$ را بدست آورد.

همچنین با توجه به اینکه در مجموع بالا عضو ‏$‎i‏$‎ با عضو $n+1-i‏$‎‎ تنها در ضریب انتهایی تفاوت دارد، پس با جمع زدن عبارت بالا با ترتیب برعکس خود و تقسیم بر دو می‌توان ضریب ‏$‎i‏$‎ را از داخل جمع حذف کرد و یک ضریب ‏$(n+1)/2‏$‎‎ به بیرون جمع اضافه کرد:

$$ F(n) = \frac{n+1}{2} \sum_{i=1}^n ‎{n-1 \choose i-1} \cdot F(i-1) \cdot F(n-i) $$

که این مقاله این رابطه بازگشتی را حل کرده و حاصل آن $(n+1)^{n-1}‏$‎ می‌شود.

راه‌حل سوم

مشاهده. یک دنباله‌ی تخصیص مطلوب است اگر و تنها اگر تعداد به ازای $k=1...n$، تعداد راننده‌هایی که جای مورد علاقه‌های آن‌ها یکی از $k$ خانه‌ی آخر است کمتر یا مساوی $k$ باشد.

با استفاده از این مشاهده می‌توانیم رابطه‌ای بازگشتی برای $G(n,x)$، تعداد دنباله تخصیص‌های مطلوب برای $n$ راننده با استفاده از فقط $x$ خانه اول، به دست بیاوریم. در اینصورت پاسخ مساله‌ی اصلی برابر با $G(n,n)$ خواهد شد.

• حالت پایه: $G(n, 1)=1$، زیرا طبق تعریف G در این حالت فقط یک خانه (خانه‌ی اول) را می‌توان به $n$ راننده اختصاص داد، پس فقط یک حالت تخصیص مطلوب $\{1,...,1\}$ داریم.
• حالت کلی: فرض کنید می‌خواهیم تعداد حالت‌هایی که خانه‌ی $x$ به دقیقا $i$ نفر تخصیص داده شده است را بشماریم. طبق مشاهده‌ی بالا $i$ حداکثر $n-x+1$ می‌تواند باشد. این $i$ نفر را به ${n \choose i}$ طریق می‌توانیم انتخاب کنیم و پس از اینکه خانه‌ی $x$ را به عنوان خانه‌ی مورد علاقه‌ی این $x$ نفر تخصیص دادیم، به بقیه‌ی $n-i$ راننده‌ی باقی‌مانده باید خانه‌هایی از $x-1$ خانه‌ی اول به عنوان خانه‌ی مورد علاقه تخصیص دهیم، یعنی $G(n-i,x-1)$ حالت. یعنی در کل رابطه‌ی بازگشتی خواهد شد:

$$ G(n,x) = \sum_{i=0}^{n-x+1} {n \choose i} \cdot G(n-i, x-1) $$

که این رابطه بازگشتی منجر به یک الگوریتم برنامه‌سازی پویا می‌شود که با پیاده‌سازی آن در کامپیوتر برای $G(10,10)$ مقدار $11^9$ بدست می‌آید.

تناظر یک به یک با درخت‌های برچسب‌دار

طبق فرمول Cayley تعداد درخت‌های برچسب‌دار $n$ راسی برابر است با $n^{n-2}$. پس تعداد پارکینگ‌های مطلوب با اندازه $n$ که قبلا نشان‌دادیم $(n+1)^{n-1}‏$‎ است، با تعداد درخت‌های برچسب‌دار $n+1‏$‎ راسی برابر است، و به نظر می‌آید بتوان تناظر یک به یکی بین حالات این دو مساله ایجاد کرد.

در ادامه با مثال یک تناظر یک به یک ارائه می‌دهیم.

فرض کنید دنباله جاهای مورد علاقه برابر باشد با: $\{6, 1, 7, 1, 6, 1, 9, 2, 6, 3\}$ یعنی راننده‌ی اول به جای ۶ ام علاقه دارد، راننده‌ی دوم به جای یکم، ...، و راننده‌ی دهم به جای ۳ ام. در اینصورت با اجرای الگوریتم مساله، حالت پارکینگ نهایی خواهد شد $\{2, 4, 6, 8, 10, 1, 3, 5, 7, 9\}$ یعنی نفر دوم در جای یکم پارک خواهد کرد، نفر چهارم در جای دوم، و الی آخر.

اکنون به جای نفر ۱۰ ام در پارکینگ نهایی دقت کنید. راننده‌هایی که قبل از او پارک کرده‌اند حتما جای مورد علاقه‌شان کمتر یا مساوی نفر ۱۰ ام است، و راننده‌هایی که بعد از او پارک کرده‌اند حتما جای مورد علاقه‌شان بعد از نفر ۱۰ ام است. و گرنه موقع ورود نفر ۱۰ ام آن جای خاص خالی نبود.

پس می‌توانیم این مساله را به دو زیر مساله بشکنیم:

• زیر مساله ۱: نفرات $\{2, 4, 6, 8\}$ با جاهای مورد علاقه $\{1, 1, 1, 2\}$.
• زیر مساله ۲: نفرات $\{1, 3, 5, 9\}$ با جاهای مورد علاقه $\{6, 7, 6, 9, 6\}$

اکنون الگوریتم بازگشتی ساختن درخت متناظر چنین است:

ورودی الگوریتم ما عبارت است از یک گره کمکی که برچسبش بیشتر از شماره همه راننده‌ها باشد و $n$ راننده با برچسب‌هایشان و جای مورد علاقه‌شان، که این تخصیص جاهای مورد علاقه طوری است که راننده‌ها اگر به ترتیب برچسب‌هایشان وارد شوند در $n$ خانه متوالی پارک می‌کنند.

حالت پایه یک گره کمکی و صفر راننده است که درخت متناظرش برابر است با یک گره که برچسبش همان برچسب گره کمکی است.

حالا به صورت استقرایی فرض کنید درخت‌های با سایز کوچک‌تر را بلدیم بسازیم. ابتدا با استفاده از جایگاه نهایی نفر آخر مساله را به دو بخش می‌شکنیم، مثل مثال بالا. و دو زیر درخت زیر را می‌سازیم:

• درخت ۱: گره کمکی: برچسب نفر آخر. راننده‌ها: راننده‌های پارک کرده در خانه‌های قبل از نفر آخر (یعنی زیرمساله ۱ در مثال بالا)
• درخت ۲: گره کمکی: گره کمکی مسال اصلی، راننده‌ها: راننده‌های پارک کرده در خانه‌های بعد از نفر آخر (یعنی زیرمساله ۲ در مثال بالا)

مثالا اگر مثال بالا را در نظر بگیریم و گره کمکی را 11 در نظر بگیریم که بیشتر از برچسب همه‌ی راننده‌هاست،

• درخت ۱ با گره کمکی ۱۰ و نفرات $\{2, 4, 6, 8\}$ با جاهای مورد علاقه $\{1, 1, 1, 2\}$ ساخته می‌شود و خواهد شد (با توجه به اینکه بازگشتی و استقرایی به مساله نگاه می‌کنیم، فرض می‌کنیم مساله‌های با سایز کوچکتر را بلدیم):

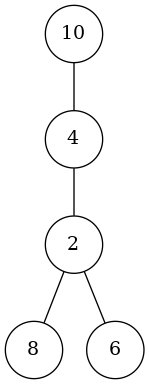
• درخت ۲ با گره کمکی مساله اصلی (۱۱) و نفرات $\{1, 3, 5, 9\}$ با جاهای مورد علاقه $\{6, 7, 6, 9, 6\}$ ساخته می‌شود و خواهد شد:

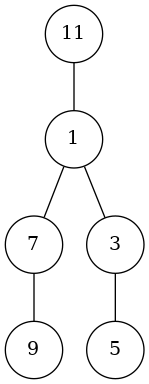
حال اگر درخت ۱ را با استفاده از هر گرهی به گره کمکی درخت راست وصلی کنیم، اطلاعات کافی برای اینکه در مساله‌ی اصلی کدام راننده‌های جای مورد علاقه‌شان قبل از راننده آخر بود را داریم: با ریشه در نظر گرفتن گره کمکی زیردرختی که شامل راننده‌ی آخر است را پیدا می‌کنیم. آن زیر درخت می‌شود درخت ۱ ای که بالا ساختیم که شامل راننده‌هاییست که جای مورد علاقه‌شان قبل از راننده‌ی آخر است.

ولی هنوز اطلاعات کافی برای اینکه جای مورد علاقه‌ی راننده‌ی آخر را بازیابی کنیم نداریم. اگر راننده آخر در جای ۵ ام پارک کرده، جای مورد علاقه‌اش هر کدام از ۵ خانه‌ی اول می‌تواند باشد. در این مثال خاص جای مورد علاقه‌اش ۳ است. برای اضافه کردن این اطلاعات به درخت، کافی است از درخت ۱ راسی را برای اتصال به گره کمکی مساله اصلی انتخاب کنیم که ترتیب آن در بین برچسب‌های درخت ۱ سوم است! یعنی در مثال بالا که اعضای درخت ۱ به ترتیب صعودی $\{2,4,6,8,10\}$ هستند، برچسب سوم می‌شود ۶. پس گره کمکی مساله اصلی که گره کمکی درخت ۲ هم بود را به گره با برچسب ۶ در درخت ۱ وصل می‌کنیم و درخت نهایی می‌شود:

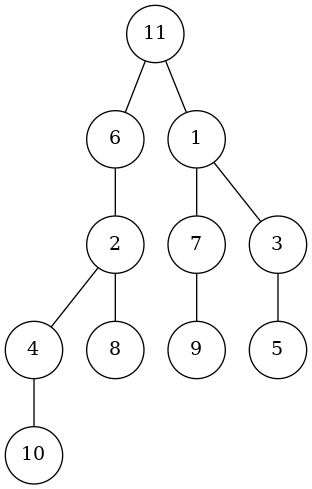
پس برای بازیابی جاهای مورد علاقه از یک درخت داده شده:

• گره با برچسب بیشینه را پیدا می‌کنیم. این گره همان گره کمکی است که استفاده کردیم.
• گره با دومین برچسب بیشینه را پیدا می‌کنیم. این گره شماره راننده آخر است.
• زیردرختی از گره کمکی که دارای گره راننده آخر را پیدا می‌کنیم. این زیردرخت زیرمساله ۱ در حالت بالا است و می‌توانیم به صورت بازگشتی اطلاعاتش را بازیابی کنیم.
• کل درخت منهای زیر درخت قبلی زیرمساله ۲ را در حالت بالا می‌دهد. اطلاعات این زیر درخت را هم به صورت بازگشتی بازیابی می‌کنیم. چون این زیردرخت شامل اطلاعات راننده‌های سمت راست راننده آخر هستند، پس از بازیابی به صورت بازگشتی، اندازه درخت چپ را به جای مورد علاقه آن‌ها اضافه می‌کنیم.
• جای مورد علاقه نفر آخر هم با استفاده از یالی که گره کمکی اصلی را به زیر درخت اول وصل کرده بازیابی می‌کنیم.

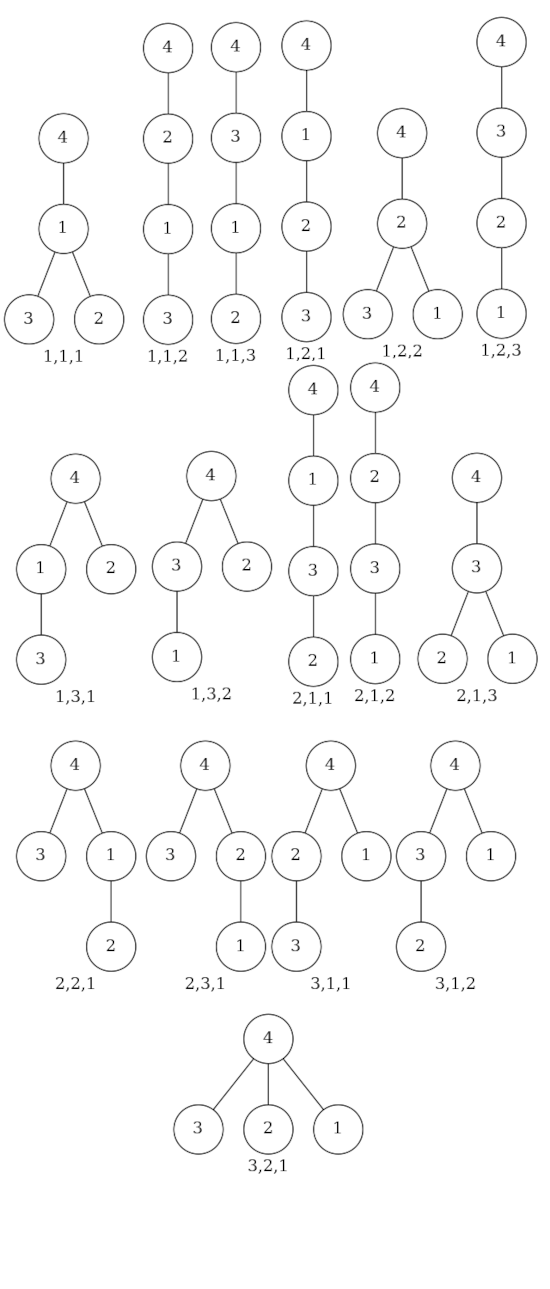
به عنوان مثالی دیگر، اگر به جای ۱۰ راننده و ۱۰ جای پارکینگ، ۳ راننده و ۳ جای پارکینگ داشتیم، پاسخ مساله $2^4=16$ می‌شد و در شکل زیر تخصیص‌های مجاز و درخت متناظر ۴ راسی آن‌ها را مشاهده می‌کنید: