تقسیم دو عدد تصادفی
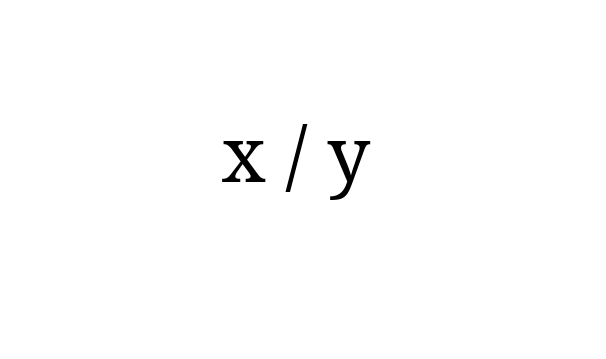
دو تا عدد تصادفی x و y بین صفر و یک به صورت یونیفرم انتخاب میکنیم. احتمال این که نزدیکترین عدد طبیعی به x/y زوج باشه چقدره؟
لینک سوال در توویتر: https://x.com/Riazi_Cafe/status/1845320177530864108
متغیر \(r = \frac{x}{y}\) را برای متغیرهای تصادفی انتخابشده \(x\) و \(y\) تعریف کنیم. همچنین تابع احتمال \(f(a,b)\) را به صورت زیر تعریف میکنیم:
\[f(a,b) = \mathsf{Pr}(a \leq r \leq b).\]
با این تعریف، پاسخ مسئله برابر با \(f(0,0.5) + f(1.5, 2.5) + f(3.5, 4.5) + \ldots\) خواهد بود. بنابراین، پاسخ نیاز به تعیین مقدار تابع \(f(a,b)\) بستگی دارد. به این منظور، دو حالت را به طور جداگانه بررسی میکنیم: 1. هر دو \(a\) و \(b\) کوچکتر از 1 باشند. 2. هر دو \(a\) و \(b\) بزرگتر از 1 باشند.
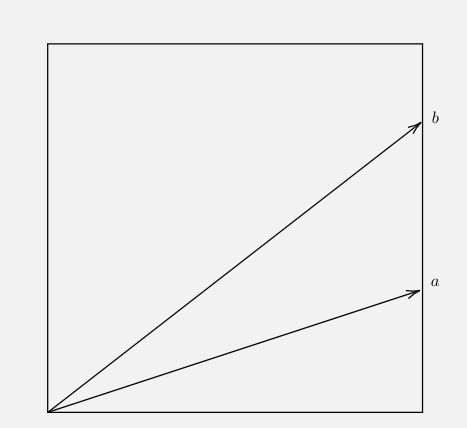
حالت (i): هر دو \(a\) و \(b\) کوچکتر از 1 هستند: در این صورت، یک نقطه \(p = (x, y)\) را در نظر بگیرید که مختصات آن برابر با \(x\) و \(y\) هستند. این نقطه در یک مربع واحد قرار دارد که نقاطی با مختصات بین 0 و 1 را پوشش میدهد. با این حال، \(\frac{x}{y}\) در بازه \([a, b]\) قرار خواهد گرفت اگر و فقط اگر نقطه روی مثلثی باشد که توسط دو پیکان ساخته شده است. از آنجایی که مساحت مثلث برابر با \(\frac{b-a}{2}\) است و مساحت مربع برابر با 1 میباشد، احتمال اینکه \(a \leq \frac{x}{y} \leq b\) برقرار باشد برابر با \(\frac{b-a}{2}\) خواهد بود.
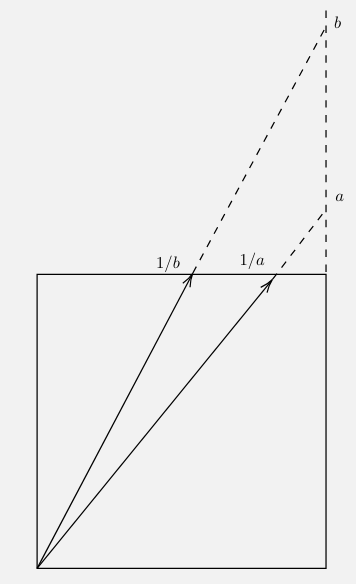
حالت (ii): هر دو \(a\) و \(b\) بزرگتر از 1 هستند. این حالت نیز مشابه حالت قبلی است، با این تفاوت که نسبت \(\frac{x}{y}\) تنها در صورتی بین \(a\) و \(b\) قرار میگیرد که نقطه \(p\) روی مثلث نشان دادهشده در شکل زیر باشد. توجه داشته باشید که مساحت این مثلث برابر با \(\frac{1/a - 1/b}{2}\) است. بنابراین، احتمال اینکه \(\frac{x}{y}\) بین \(a\) و \(b\) باشد نیز برابر با \(\frac{1/a - 1/b}{2}\) خواهد بود.
بر اساس استدلالهای فوق، پاسخ مسئله برابر است با \[\begin{aligned} f(0,0.5) + \sum_{i=1}^{\infty} f(2i-0.5, 2i+0.5) &= 0.25 + \sum_{i=1}^{\infty} \frac{1/(2i-0.5) - 1/(2i+0.5)}{2} \nonumber \\ & = 0.25 + \sum_{i=1}^{\infty} (1/(4i-1) - 1/(4i+1)) \nonumber \\ & = 0.25 + \sum_{i=2}^{\infty} (-1)^i/(2i-1) \nonumber \\ & = 0.25 + 1-\pi/4 \label{eq:one}\\ & = 1.25-\pi/4 \nonumber \end{aligned}\] که از فرمول لایبنیتس (\(\pi/4 = 1 - 1/3 + 1/5 - 1/7 \ldots\)) استفاده کردهایم.